Как построить график функции

Элементарный график изменения

График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.

Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.

Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.

2

Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.

После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.

В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая – синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.

Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.

Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».

Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» – «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.

Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам – Вкладка “Конструктор”, которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.

Настраиваем оси диаграммы в Excel

Для большинства типов диаграмм в Excel вертикальная ось (она же – ось значений или ось Y) и горизонтальная ось (она же – ось категорий или ось Х) добавляются автоматически при создании диаграммы.

Чтобы скрыть или показать оси диаграммы, кликните по иконке Элементы диаграммы (Chart Elements), затем нажмите стрелку в строке Оси (Axes) и отметьте галочкой те оси, которые нужно показать, или уберите галочку рядом с теми, которые нужно скрыть.

Для некоторых типов диаграмм, например, для , может быть показана вспомогательная ось.

При создании объёмных диаграмм, можно отобразить ось глубины:

Для каждого элемента осей диаграммы в Excel можно настраивать различные параметры (далее поговорим об этом подробнее):

Добавляем названия осей в диаграмме

Создавая диаграмму в Excel, можно добавить названия вертикальной и горизонтальной осей, чтобы пользователям было проще понять, что за данные показаны на диаграмме. Чтобы добавить названия осей, нужно сделать вот что:

1. Кликните в любом месте диаграммы Excel, затем нажмите по иконке Элементы диаграммы (Chart Elements) и поставьте галочку в строке Названия осей (Axis Titles). Если нужно показать название только для одной из осей (либо вертикальной, либо горизонтальной), нажмите стрелку справа и уберите одну из галочек.
2. Кликните на диаграмме по текстовому полю названия оси и введите текст.

Чтобы настроить оформление названия оси, кликните по нему правой кнопкой мыши и в контекстном меню нажмите Формат названия оси (Format Axis Title). При этом откроется одноимённая панель с большим выбором настраиваемых параметров оформления. Можно также использовать параметры, предложенные на вкладке Формат (Format) Ленты меню, как мы делали при .

Связываем названия осей с заданными ячейками рабочего листа

Как и , название оси можно связать с заданной ячейкой рабочего листа при помощи ссылки, чтобы это название обновлялось автоматически при изменении данных в связанной ячейке.

Чтобы создать такую ссылку, выделите название оси и в строке формул введите знак равенства (=), затем кликните по ячейке, с которой нужно связать название оси, и нажмите Enter.

Изменяем масштаб оси диаграммы

Microsoft Excel автоматически определяет минимальное и максимальное значения, а также единицы измерения для вертикальной оси, основываясь на том, какие данные использованы для построения диаграммы. При необходимости для вертикальной оси можно настроить собственные более подходящие параметры.

1. Выделите вертикальную ось диаграммы и щелкните по иконке Элементы диаграммы (Chart Elements).
2. Нажмите стрелку в строке Оси (Axis) и в появившемся меню выберите Дополнительные параметры (More options). Откроется панель Формат оси (Format Axis).
3. В разделе Параметры оси (Axis Options) сделайте одно из следующих действий:
   • Чтобы задать начальное и конечное значения вертикальной оси, введите соответствующие значения в поля Минимум (Minimum) или Максимум (Maximum).
   • Чтобы изменить масштаб оси, введите значения в поля Основные деления (Major) и Промежуточные деления (Minor).
   • Чтобы отложить значения по оси в обратном порядке, отметьте галочкой параметр Обратный порядок значений (Values in reverse order).

Горизонтальная ось, в отличие от вертикальной, чаще имеет текстовые подписи данных, а не числовые, поэтому настроек масштаба у этой оси меньше. Однако можно изменить количество категорий, которые будут показаны между метками, порядок категорий и точку, где две оси пересекаются:

Изменяем числовой формат у подписей оси

Если нужно, чтобы числа в подписях оси отображались как валюты, проценты, время или в каком-либо другом формате, кликните по подписям правой кнопкой мыши и в контекстном меню нажмите Формат оси (Format Axis). В открывшейся панели перейдите в раздел Число (Number) и выберите один из доступных числовых форматов:

Совет: Чтобы установить для чисел формат исходных данных (тот, что в ячейках рабочего листа), поставьте галочку Связь с источником (Linked to source). Если не получается найти раздел Число (Number) в панели Формат оси (Format Axis), проверьте, что на диаграмме выделена ось значений (это, как правило, вертикальная ось).

Aiportal.ru

Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.

Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций, а также по перечню поддерживаемых функций и константных значений.

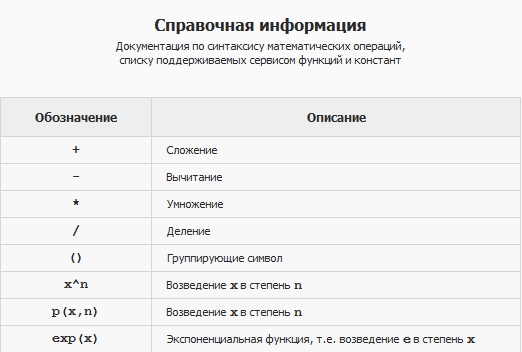
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.

Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.

Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.

Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.

Для построения графика достаточно лишь иметь выход в сеть с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.

Kontrolnaya-Rabota.ru

• Построение двухмерного графика функции в декартовых и полярных координатах.
• Построение графика, заданного параметрически.
• Построение 3D графиков (поверхностей), заданных уравнением.
• Построение гистограмм и графиков и по точкам.
• Построение графиков неявно заданных функций.

Пользователю достаточно ввести в онлайн-программу данные из условия задачи и кликнуть кнопку «Построить график».

Запутаться сложно, так как каждая страница этого раздела сопровождается пояснениями и примерами. Там же даны подсказки, какие символы и сокращения следует использовать при вводе выражений.

При построении 2D-графика в декартовых координатах приводится подробный результат исследования функции, чего не встретишь практически нигде.

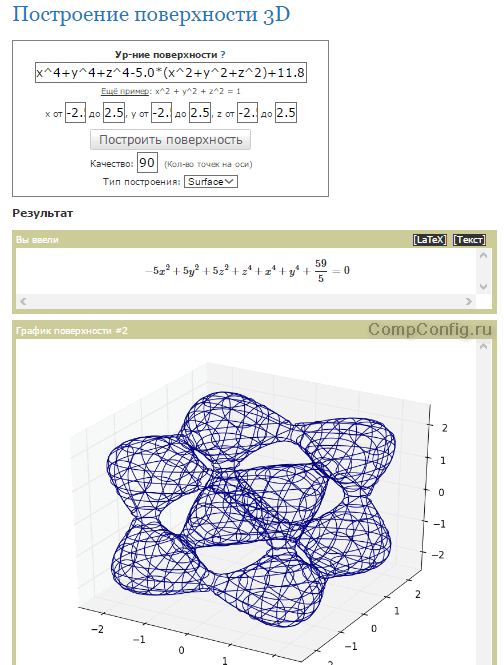
Достоинства сервиса kontrolnaya-rabota.ru — возможность пользоваться им без ограничений, выдача результатов с ходом решения, быстрые и точные ответы, наличие других онлайн-калькуляторов для вычисления уравнений, интегралов, неравенств и прочего. А недостаток — в том, что не все чертежи можно масштабировать. Это создает определенные неудобства при копировании.

Квадратичная функция — формула, свойства и виды графиков

Раздел «Квадратичная функция», ее свойства и график проходят в средней школе в 8 — 9 классах. Но не все учителя объясняют доступно. А вышедшим из ученического возраста может понадобиться обновить познания. 

Поэтому рассмотрим простые примеры построения графиков квадратичной функции.

Определение и формула квадратичной функции

Квадратичной называют функцию канонического вида:

• a, b – коэффициенты;
• с – свободный член.

Формально конструкция именуется «квадратный трехчлен». Сразу заметно, что область определения не ограничена, а четность не выявлена.

График функции при а = 1, b = c = 0

Наиболее тривиальная, но наглядная и информативная разновидность с формулой:

y = x2

Функция четная, возрастающая. Построим по точкам.

Получившаяся кривая называется «парабола». Характерна для уравнений с «квадратом».

Нижнюю точку с координатами (0; 0) называют «вершиной». Единственное место, где одной функции соответствует один аргумент. В данном случае – это минимум функции.

Уходящие вверх части кривой – «ветви». На всех участках кроме вершины к одному (y) относятся сразу (±x).

Вывод: ветви данной параболы имеют ось симметрии — вертикальную прямую ординат Y.

График функции, когда b = c = 0, а > 1 и а

• Кривая задается, например, так:
• y = 2×2
• Ветви «сожмутся» относительно оси симметрии.

1. Построим другой график.
2. y = 0,5×2
3. Ветви «разойдутся».

• Куда интереснее переместить коэффициент a в отрицательную область.
• y = -x2

Парабола «повернется» на 180°. И вершина станет максимумом.

График функции при b = 0, с ≠0

1. Рассмотрим такой вариант:
2. y = x2 + 1
3. Вершина сдвинется на величину c по оси Y.

• А если параметр c отрицателен? Уравнение выглядит так:
• y = x2 — 1
• Смещение произойдет ниже точки (0; 0).

Пересечения с осью абсцисс (y = 0)

1. Иными словами, следует решить уравнение:
2. ax2 + bx + c = 0
3. Корнями уравнения будут:

Подкоренное выражение называется «дискриминант» и обозначается «D». Появляются варианты:

1. D отрицателен, D > 0. В таком случае действительные корни не существуют. Парабола не пересекает ось Х.

2. D положителен, D > 0. Существуют оба корня. Кривая пересекает X в двух известных местах.

3. D = 0. Корень один – -b/2a. Пересечение единственно. А такое возможно в одном случае: найденное означает абсциссу вершины.

Вершина

Горизонтальная координата вычисляется по формуле:

Вертикальная:

Касательная в вершине параболы совпадает с осью X или параллельна ей. Значит тангенс её относительного наклона равен 0. А это производная функции:

Нашли x0, а y0 находится подстановкой в уравнение найденного.

Приблизительный вид

По уравнению можно прикинуть общую картину:

• положительное значение коэффициента a говорит о направленности ветвей вверх и наоборот;
• по дискриминанту определим расположение относительно X;
• находим пересечения (если есть).

Пример построения графика

1. Дано:
2. y = x2 + 2x — 3
3. Проанализируем:

• a = 1, положительный, поэтому ветви параболы направлены вверх;
• b = 2;
• с = -3.

• Алгоритм построения графика квадратичной функции:
• 1. Находим вершину:

1. 2. Определяем точки пересечения с осью X:

3. Посчитав еще 2 — 3 точки правее и левее оси симметрии x = -1, получим достоверный график.

Свойства параболы

Основные свойства следующие:

1. Область определения – все действительные числа.

2. Вершина является минимумом при положительном коэффициенте x2, максимумом – при отрицательном.

3. Координаты вершины зависят только от коэффициентов.

4. Ось симметрии проходит через вершину и параллельна оси ординат.

Заключение

В интернете существует масса онлайн-калькуляторов для облегчения работы с кривой. Приведенные же приемы и перечисленные свойства позволяют лучше понять сущность квадратичного выражения.

Параболические отражатели позволяют получать параллельный пучок света от точечного источника. Антенна такого типа позволяет концентрировать и усиливать радиосигнал. Не абстрактная линия на бумаге.

Особенности оформления графиков в Excel

Несколько советов по оформлению графиков в Excel:

Первое, что следует сделать пользователю, — ввести правильно название зависимости. Для этого нужно выделить щелчком мыши блок «Название диаграммы», щёлкнуть по нему ещё раз и ввести требуемое наименование. При необходимости этот блок можно удалить, выделив его и нажав клавишу Delete.

Если требуется изменить не только название, но и стиль написания, следует, снова выделив блок, вызвать контекстное меню и выбрать в нём раздел «Шрифт». Подобрав подходящий вариант, юзер может нажимать на «ОК» и переходить к дальнейшим действиям.

Вызвав меню «Формат названия диаграммы», можно определить, в какой части рисунка будет располагаться наименование: в центре, в левом верхнем, нижнем правом углу и так далее.

Чтобы добавить на график названия осей, следует щёлкнуть мышью по «плюсику» справа от рисунка и в выплывающем списке установить галочку в соответствующем чекбоксе.

Если изначальное расположение названий не устраивает пользователя, он может свободно перетаскивать их по полю графика, а также менять их наименования описанным ранее способом.

Чтобы добавить на любую линию графика подписи (размещаются прямо на сетке) или выноски данных (в отдельных окошечках), нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню «Добавить подписи данных».

Юзер может свободно сочетать способы размещения подписей, выбирая любой из пунктов в расширенном меню окошка «Элементы диаграммы».

Выбрав в том же меню «Дополнительные параметры», в боковом меню следует указать категорию представленных данных: простые числа, дроби, проценты, деньги и так далее.

Чтобы добавить таблицу с данными непосредственно на график, нужно вызвать нажатием на «плюсик» всё те же «Дополнительные параметры» и установить галочку в одноимённом чекбоксе.

Сетку, позволяющую найти значения графика в каждой точке, с помощью того же меню можно совсем убрать или добавить на неё основную и вспомогательную разметку.

«Легенда» — не самый полезный, но привычный блок графиков Excel. Убрать или перенести его можно, сняв галочку в окне «Дополнительные параметры» или вызвав вложенное меню. Более простой вариант — выделить блок щелчком мыши и нажать клавишу Delete или перетащить по полю графика.

Понять общее направление движения графика поможет линия тренда; добавить её для каждого ряда значений можно в том же окне.

Перейдя на вкладку «Конструктор», пользователь может кардинально изменить вид графика, выбрав один из стандартных шаблонов в разделе «Стили диаграмм».

А вызвав находящееся там же меню «Изменить цвета» — подобрать палитру для каждой линии в отдельности или для всего графика в целом.

Меню «Стили» вкладки «Формат» позволяет найти оптимальное представление для текстовых элементов графика.

Изменить фон, оставив нетронутым тип диаграммы, можно с помощью раздела «Стили фигур».

На этом настройку графика можно считать оконченной. Пользователь может в любой момент изменить тип диаграммы, перейдя в одноимённое меню и выбрав понравившийся вариант.

Как чертить график в ворде. Графики и диаграммы в Microsoft Word

13.07.2019

Здравствуйте, друзья! Сегодня я поделюсь с вами информацией, как построить в ворде график функции.

В Интернете много примеров построения диаграмм с использованием ворда и экселя, но данные приемы не всегда могут соответствовать конечному результату.

Например, чтобы построить график функции по точкам, нужно заполнить таблицу данными, затем построить диаграмму типа График. Далее необходимо провести кучу дополнительных настроек, чтобы привести этот график к нужному виду.

И скажите, зачем столько трудностей, когда нужен всего-то рисунок этого графика для иллюстрации функции. Следовательно, проще взять и нарисовать этот график средствами векторного редактора, встроенного в Word.

Итак, на примере параболы разберем, как построить в ворде график этой функции. Если быть кратким, то сначала нарисуем график, а потом сохраним его как картинку и вставим в нужный документ. Я использую версию Word 2010, но все шаги вполне применимы и в , так как отличия в интерфейсе минимальны.

Как построить в ворде график функции по точкам

Создадим новый документ (Файл – Создать – Новый документ – Создать).

Для рисования графика по точкам, хорошо бы воспользоваться сеткой. Влючаем её.

Включение вспомогательной сетки в Microsoft Word

На вкладке Вид в разделе Показать ставим галочку напротив пункта Сетка. Теперь гораздо проще будет рисовать координатные оси и сам график.

Рисуем оси координат

На вкладке Вставка в разделе Фигуры-Линии выбираем Стрелку. Курсор примет вид креста. При нажатой левой кнопке мыши растягиваем стрелку до нужной длины.

При выделенной фигуре, на ее концах есть кружки. Потянув за любой из них, при нажатой левой кнопке мыши, можно изменить длину или направление стрелки.

Для рисования второй оси проделываем шаги, описанные выше.

Далее определяем на нашей сетке единичный отрезок и обозначаем его с помощью надписи (Вставка – Надпись – Нарисовать надпись). Растягиваем небольшой прямоугольник и вписываем в него цифру 1.

Теперь убираем заливку и контур у надписи (фигура Надпись должна быть выделена).

Установка единичного отрезка на оси координат

Остается только перенести цифру поближе к нужному месту.

Если скопировать эту надпись и вставить несколько раз, то можно будет заменив единичку, подписать оси координат, указать начало координат и расставить еще несколько значений на осях.

Ну, вот, координатная плоскость задана.

Рисуем график параболы у=х 2

В фигурах выбираем Кривая и на нашей координатной плоскости делаем одним кликом первую точку(-3,9), следующий клик в точке(-2,4), следующий в точке (-1,1) и так далее. На последней точке делаем двойной клик, чтобы завершить рисование кривой. Желательно постараться проставить все нужные точки графика за один проход.

Рисование графика инструментом Кривая

Но если не получилось, не беда, все можно поправить. Кликните на вашу кривую правой кнопкой мыши и в контекстном меню вы берите пункт Начать изменение узлов.

Коррекция узловых точек графика

Ваши узловые точки будут доступны для перемещения, можно скорректировать кривизну или длину кривой. Используя контекстное меню для кривой, узлы можно добавить или удалить.

Изменить цвет графика и его толщину можно в ленте меню Средства рисования – Формат и в разделе Стили фигур.

Помните! Режим сетки распространяется на все страницы документа. После его отключения, сетка на графике тоже исчезнет.

Совет! Делайте графики в отдельном документе, в целевой текст вставляйте скриншоты. Так у вас будет возможность исправить неточности и поменять рисунок.

Теперь, когда график готов, нужно сделать его скриншот и вставить в нужный документ.

Как сделать скриншот в ворде

Изменяем масштаб страницы так, чтобы рисунок графика занял максимальную область экрана. На клавиатуре нажимаем кнопку PrintScreen(PrtSc). Затем идем в нужный документ указываем место для вставки и даем команду Вставить из вкладки на ленте инструментов или из контекстного меню. Вставится все содержимое экрана с ненужными нам частями.

PS: Интересные факты

Дорогой читатель! Вы посмотрели статью до конца.Получили вы ответ на свой вопрос?

Видеоинструкция

Для тех, у кого остались какие-нибудь вопросы по описанной выше инструкции, ниже прилагается видеоматериал с дополнительными пояснениями.

Диаграммы в Microsoft Word являются отличным средством для визуализации и наглядного представления сложно воспринимаемых объемов числовой информации в тексте. Диаграммы позволяют четко проследить закономерности, соотношения фактических величин, выявить тенденции и логические последовательности в массивах данных. Microsof Word из пакета Office предоставляет достаточный набор инструментов для быстрого создания диаграмм всех распространенных типов.

Как сделать диаграмму в ворде
редактора MicrosoftWord диаграммы

1. Установите курсор в то место документа, в которое необходимо добавление диаграммы.
2. В главном меню программы выберите пункт «Вставка», в котором активируйте вкладку «Диаграмма».
3. В правой части появившегося окна выберите нужный тип диаграммы. Основные типы доступных диаграмм, которые наиболее часто используются в зависимости от поставленных целей:
   • Графики
     – диаграмма в виде графика позволит вам наглядно продемонстрировать динамику изменения определённого значения в зависимости от определенного показателя. Изменение дохода по месяцам, производительности по различным годам — типичные области использования графиков.
   • Круговая
     диаграмма используется для того, чтобы показать соотношения нескольких величин, объединенных определенным общим параметром. К примеру, с ее помощью можно показать доли людей разных национальностей в пределах одного государства, соотношение различных источников дохода в общей массе прибыли.
   • Гистограмма
     – позволит показать изменение соотношения устойчивых групп определенных величин в зависимости от какого-либо фактора. К примеру, отношение стоимости евро к доллару, доллара к рублю сегодня, неделю назад, две недели, три и так далее. Это достаточно сложный тип диаграмм, который формируется, исходя из значений из пяти столбиков, в которых занесена информация по объёму, самому низкому курсу, самому высокому курсу, курсу закрытия и курсу открытия.
   • Биржевая
     диаграмма используется брокерами, для наглядности изменений в росте-падении цен на акции компаний, или курсах валют. Биржевые диаграммы позволяют отслеживать связи сразу нескольких величин, в зависимости от выбранного показателя в роли которого чаще всего выступает время. Например, на одном графике можно представить суточную динамику по объемам продаж, с одновременным контролем максимальной и минимальной цен продажи с указание стоимости отслеживаемых позиций на момент закрытия.
   • Поверхность
     в виде диаграммы чаще всего используется в научной деятельности для отображения трехмерных моделей различных процессов.

   Другие типы диаграмм являются либо разновидностями уже рассмотренных, либо используются значительно реже.

4. После выбора типа диаграммы нажмите на кнопку «Ок» после чего пример диаграммы появится в вашем документе. Одновременно откроется лист значений в Excel, на основании которых построена данная диаграмма. Ваша задача состоит в том, чтобы отредактировать данные на листе, замени показатели на свои значения. После ввода каждого нового значения в Excel график в Word будет автоматически перестраиваться и вам нужно только следить за правильностью ввода информации. После занесения всех данных окно Excel можно закрыть.
5. Завершающим этапом создания диаграммы является оформление. К диаграмме можно добавить название, произвести точную настройку различных параметров оформления диаграммы. Для этого поместите курсор в область диаграммы и когда он примет вид крестика из стрелочек, нажмите правую кнопку мышки. В появившемся контекстном меню выберите необходимый пункт.

текстовой формами

Иногда, работая в программе Microsoft Office Word, нужно срочно построить график. Многие пользователи для этого открывают другие программы, поскольку не знают, как построить график в Word. Однако делается это довольно быстро, главное знать какие вкладки задействовать.

Общие рекомендации по созданию графиков

Есть несколько рекомендаций, как правильно создавать графики, чтобы они были читаемыми и информативными:

Не нужно использовать слишком много линий. Достаточно лишь двух-трех
Если необходимо отобразить больше информации, лучше создать отдельный график.
Нужно особое внимание уделить легенде, а также осям

От того, насколько качественно они подписаны, зависит то, насколько легко будет читать график
Это важно, поскольку любая диаграмма создается для упрощения представления определенной информации, но если подойти к этому безответственно, человеку будет тяжелее разобраться.
Несмотря на возможность настраивать внешний вид диаграммы, не рекомендуется использовать слишком много цветов. Это будет сбивать с толку человека, читающего диаграммы.

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: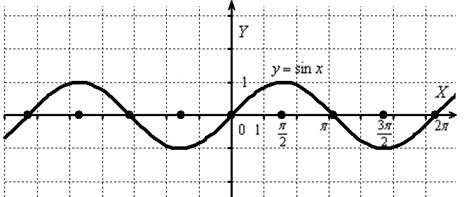
Согласно правилу, при  график сохраняется: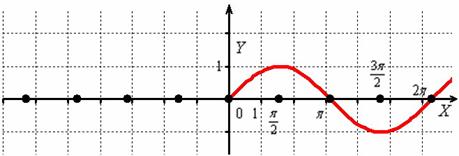
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: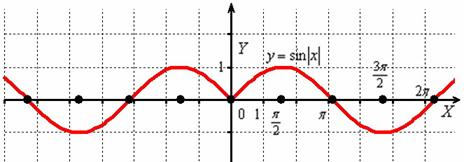

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае: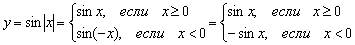

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: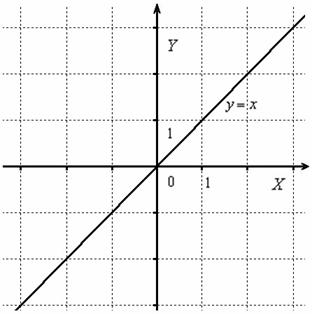
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: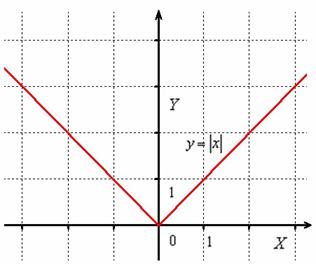

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)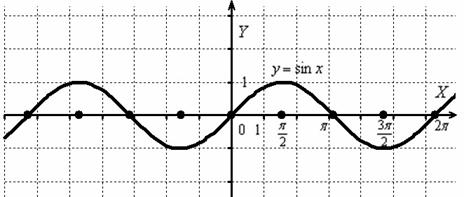

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :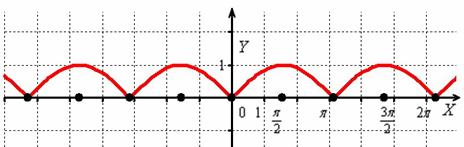

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем: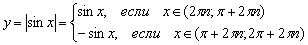, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)