Знаки больше и меньше в математике — сравнение чисел с примерами

Типография и внешний вид

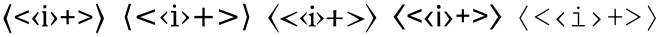
Угловые скобки , символы сравнения и простые гильеметы (полукруглые символы) в шрифтах Cambria, DejaVu Serif, Andron Mega Corpus, Andika и Everson Mono

Знаки «меньше» и «больше» состоят из линии, изогнутой посередине с прямыми участками, при этом угол перегиба обычно острый (то есть меньше прямого). Концы перпендикулярны друг другу, чтобы ноги были равной длины; в основном это выделено курсивом . Высота и положение знаков обычно соответствуют положению знака плюс . Поэтому в большинстве шрифтов они значительно больше, чем Guillemets (заостренные символы), и, с другой стороны, значительно меньше, чем угловые скобки . Последние также отличаются тем, что у них гораздо более открытый угол на изгибе, в большинстве случаев намного больше, чем прямой угол.

Равенства и неравенства

Для записи результата сравнения чисел используются следующие знаки:

=,   >   и   <.

При записи сравнения эти знаки располагают между числами.

Первый знак  =  называется знаком равенства и заменяет собой слово равно или равняется. Например, если числа  a  и  b  равны, то пишут  a = b  и говорят:  a  равно  b.

Запись, которая состоит из математических выражений, между которыми ставится знак  =  называется равенством.

Пример.

4 = 4  — равенство.

2 + 3 = 5  — равенство.

2 + 2 = 1 + 1 + 2  — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).

Равенства могут быть как верными (например,  5 = 5  — верное равенство), так и неверными (например,  11 = 14  — неверное равенство).

Два других знака  >  и  <  называются знаками неравенства и означают: знак  >  — больше, а знак  <  — меньше. Например, если число  a  больше числа  b,  то пишут  a > b  и говорят:  a  больше  b  или пишут  b < a  и говорят:  b  меньше  a.

Знаки  >  и  <  должны быть обращены остриём к меньшему числу.

Запись, которая состоит из математических выражений, между которыми ставится знак  >  или  <  называется неравенством.

Пример.

5 > 4  — неравенство.

2 < 7  — неравенство.

2 + 3 < 7  — неравенство (подобные записи представляют собой неравенство двух числовых выражений, и означают неравенство значений этих выражений).

Неравенства могут быть как верными (например,  2 < 9  — верное неравенство), так и неверными (например,  5 > 8  — неверное неравенство).

Кроме неравенств со знаками  >  и  <, которые называются строгими, используются нестрогие неравенства, для которых введены знаки  &ges;  и  &les;.  Знак  &ges;  читается больше или равно, знак  &les;  — меньше или равно. Нестрогое неравенство допускает случай равенства левой и правой его частей. Так, например,  7 &les; 7  — верное неравенство.

Также для записи неравенства двух натуральных чисел может применяться знак  ≠.  Знак  ≠  читается не равно. Например, запись  a ≠ b  — означает  a  не равно  b.

Обычно, если не оговорено иное, понятие неравенства относится только к записям со знаками  >,  <,  &ges;  и  &les;.

Ставим символы, которых нет на клавиатуре

Вариант 1: Word и его аналоги

Если у вас на компьютере установлена современная версия Word — то найти большинство самый популярных символов проще простого!

Необходимо зайти в меню «Вставка/Символы/Символы» (см. пример на скриншоте ниже ).

Если на рабочем ПК MS Office нет — хорошим вариантом может стать сервис Яндекс-Диск (прим.: там есть встроенная онлайн-версия Word). Меню выглядит аналогично вышеприведенному.

Яндекс-Диск — создать Word-документ

Кстати, как еще одной неплохой и бесплатной альтернативой Office — могу порекомендовать пакет LibreOffice. Вместо Word там используется редактор Writer.

Запустив эту программу и зайдя в меню «Вставка / Специальные символы» — вы найдете тысячи всевозможных знаков.

Writer — вставка символов

Вариант 2: готовая табличка с популярными знаками

У меня есть подготовленная небольшая табличка () со всеми самыми нужными символами: она покрывает 98% всех популярных офисных задач.

Рекомендую вам ее скопировать к себе во вспомогательный документ Word, и когда понадобиться какой-нибудь символ — просто выделить его и скопировать из нее (сочетание для копирования: Ctrl+C; для вставки: Ctrl+V).

Источник

Знаки больше или равно и меньше или равно на клавиатуре в Windows

На клавиатуре клавиш со знаками нет, поэтому для их написания в Ворде применяются различные методы:

• сочетания клавиш Alt + Num;
• сочетания клавиш Alt + X;
• символы Word;
• символы Windows.

Сочетание клавиш Alt + Num

1. Для написания знака ⩾ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 1 0 8 7 8 . Отпустите Alt — получится знак ⩾.

Для написания знака ⩽ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 1 0 8 7 7 . Отпустите Alt — получится знак ⩽.

2. Для написания знака ≥ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 8 8 0 5 . Отпустите Alt — получится знак ≥.

Для написания знака ≤ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 8 8 0 4 . Отпустите Alt — получится знак ≤.

3. Для написания знака ≧ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 8 8 0 7 . Отпустите Alt — получится знак ≧.

Для написания знака ≦ следует одной рукой нажать клавишу Alt и, удерживая её, другой рукой ввести на клавиатуре цифры 8 8 0 6 . Отпустите Alt — получится знак ≦.

Сочетание клавиш Alt + X в Microsoft Word

1. В месте знака ≥ напечатайте 2265, переведите клавиатуру на английскую раскладку и нажмите одновременно Alt и X — появится знак больше или равно.

В месте знака ≤ напечатайте 2264, переведите клавиатуру на английскую раскладку и нажмите одновременно Alt и X — появится знак меньше или равно.

2. В месте знака ≧ напечатайте 2267, переведите клавиатуру на английскую раскладку и нажмите одновременно Alt и X — появится знак больше или равно.

В месте знака ≦ напечатайте 2266, переведите клавиатуру на английскую раскладку и нажмите одновременно Alt и X — появится знак меньше или равно.

Для ноутбуков, у которых на клавиатуре нет цифрового блока, нужно дополнительно нажать клавишу Fn и использовать функциональные клавиши с цифрами.

Знаки ≥, ≧, ≤, ≦ в символах Word

Устанавливаем курсор в нужное место текста → вкладка Вставка → Символ → Другие символы… → Набор: математические операторы. Выделяем символ больше или равно или меньше или равно → Вставить.

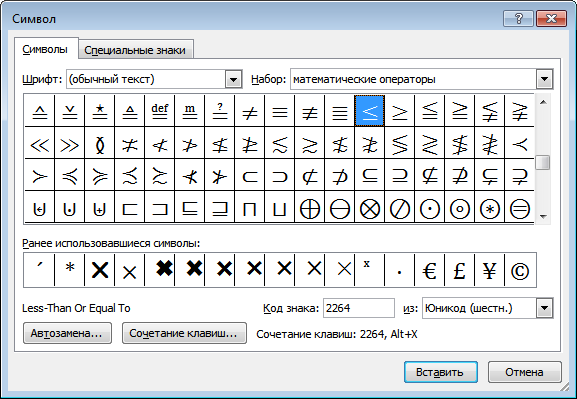
Знак в таблице символов Windows

Открываем программу символов. Для её вызова нажимаем Пуск → Выполнить → charmap.exe → ОК.

В окне таблицы найдите значок больше или равно и меньше или равно. Выделите его, нажмите кнопку Выбрать и Копировать.

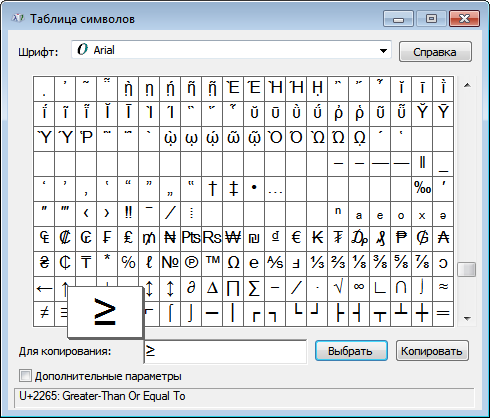
Остаётся лишь вставить символ в нужное место сочетанием клавиш Ctrl и V .

Где на клавиатуре знак приблизительно (примерно равно)?

На обычной клавиатуре знак

Конечно, для набора таких знаков существуют специальные буквенные комбинации. Для примерно равно это Alt (нажать и держать) + (в раскладке латиницей) 008776 (в такой же раскладке) и получится ≈.

Гораздо проще пойти в специальные знаки и найти значок там в шрифте Ариал (Arial), прокрути почти до самого конца:

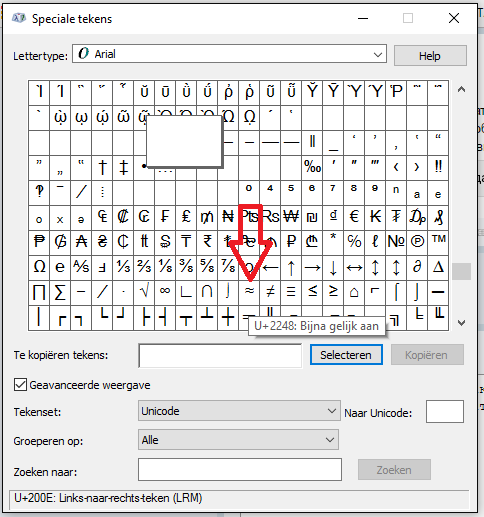
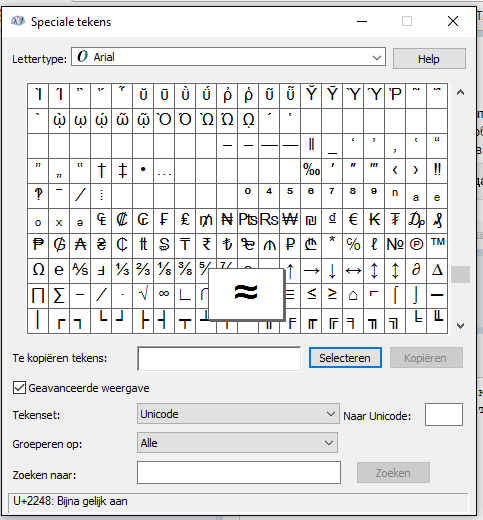
А ещё проще скопировать здесь и держать закладку на этой странице. Поверьте, я так поступаю почти со всеми сложными знаками, потому что помнить комбинации и бесконечно искать в таблице — не самый удобный метод. Я замучилась с ними и считаю, что иногда быть блондинкой — просто полезно для здоровья и внутренней гармонии.

В математике довольно часто используется знак приблизительно (примерно равно), он выглядит следующим образом:

На клавишах клавиатуры знака приблизительно нет, тем не менее его всё же можно набрать с помощью клавиатуры.

Здесь нам помогут Alt-коды: данному знаку соответствует код 008776.

Ввести этот код нужно вот так:

1) Сначала нужно удостовериться, что у вас включена цифровая клавиатура (она активируется нажатием клавиши Num Lock).

2) Зажмите клавишу «Alt».

3) На цифровой клавиатуре поочерёдно введите шесть цифр: 0, 0, 8, 7, 7 и 6.

4) Отпустите клавишу «Alt».

Если вы работаете в Ворде, то проще не набирать указанный Alt-код, а воспользоваться конструктором формул.

1) Откройте панель «Вставка» и нажмите на «Формула».

2) В документе появится «Место для формулы» и станет активной вкладка «Конструктор»: на этой вкладке в разделе «Символы» имеется знак «≈».

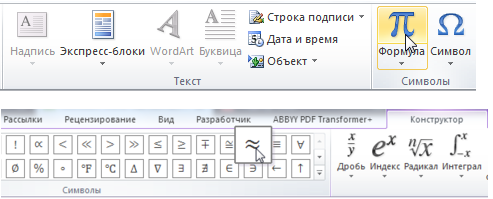
Также расскажу, как поставить знак приблизительно на клавиатуре Андроид (возможно, кому-нибудь окажется полезным).

1) Сначала переключитесь на специальную клавиатуру с цифрами и символами — для этого нажмите на «?123»:

2) Теперь нужно открыть список дополнительных символов — нажмите на «=

Нет на клавиатуре такого знака (символа). «Примерно равно» — это две волнистые черточки, одна над другой расположенные. На клавиатуре же имеется только символ с одной такой черточкой. Тильдой называется, под Esc располагается. С буквой Ё одну клавишу делит.

На клавиатуре знака «приблизительно» («примерно») ни на одной из клавиш вы не обнаружите. Действительно, одинарный знак «

« под названием «тильда» на «клаве» имеется, а находится он на одной клавише с буковкой «Ё» (для его набора нужно сменить язык на английский). Но согласитесь, тильда — это совсем не то, что нам нужно.

И хотя значок «приблизительно» на клавиатуре не значится, его все-таки можно напечатать без сложных переходов через кнопку «Пуск». Для того чтобы изобразить значок нужно воспользоваться специальным числовым кодом.

Попробуйте в Ворде сделать следующее: зажимаем кнопку Alt и удерживаем её, а другой рукой выводим «+», а затем код «008776» и получаем искомый знак.

«Alt» + «+» + «008776» = «≈»

История

Самое раннее известное использование символов < и > найдено в Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas ( Аналитическое искусство, применяемое к решению алгебраических уравнений ) Томаса Харриота , опубликованном посмертно в 1631 году. В тексте говорится: « Signum majoritatis ut a> b сигнификат a majorem quam b »и« Signum minoritatis ut a <b сигнификат a minorem quam b ».

По словам историка Арта Джонсона, когда Харриот исследовал Северную Америку, он увидел индейца с символом, который напоминал знак «больше», как в обратной, так и в прямой форме. Джонсон говорит, что, вероятно, Харриот развил два символа из этого символа.

Ход урока

2. Основная часть:

Учитель:
А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?

Ученики:
Решаем, считаем, пишем, думаем…

Учитель:
А как вы думаете, что мы будем делать сегодня?

Учитель:
Чтобы полёт прошёл удачно, необходимо быть:

• Внимательными
• Точно и правильно выполнять задания
• Не допускать ошибок, иначе ракета может потерпеть аварию.

Учитель:
Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)

• Счёт цепочкой до 10.
• Начинает учитель, дети продолжают.
• Отсчёт в обратном направлении.
• Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!

Учитель:
Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?

Ученики:
геометрические фигуры.

Учитель:
Что это за фигуры, назовите.

Ученики:
отрезок, прямая, точки, ломаная, кривая.

Учитель:
Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.

Учитель:
Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.

• Какое число идёт при счёте за числом 3, 6, 9?
• Какое число стоит перед числом 2, 5, 8, 10?
• Назовите соседей числа 2, 7?

Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)

2 3=5		4 =2
5 1=4		1+ =4
3+ =5		5- =4

Молодцы! Пульт исправен.

Учитель:
Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».

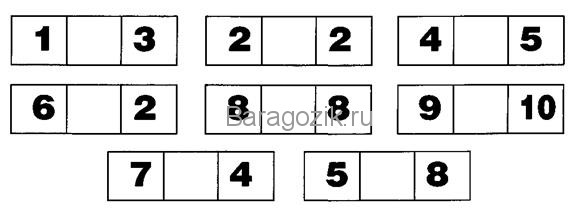
Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.

Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)

Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.

Физминутка: (негромко звучит весёлая музыка)

Учитель:
А сейчас приготовьте свои квадраты. Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.

Каких квадратов меньше?

Какое число меньше 2 или 3?

В математике есть специальная запись. Это записывают так: 2

Каких квадратов больше? (синих)

Какое число больше? (3)

Кто догадался, как это записать? 3>2

> – знак больше

Знак ставится так, чтобы к большему числу «клювик» был открыт.

Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).

• Сколько было птичек на первой картинке
• Сколько прилетело
• Сколько стало
• Их стало больше или меньше
• Как это записали, прочитайте
• Сколько ягод на кисточке
• Что произошло с ягодами
• Как это записать
• Какое число больше, меньше?

Учитель:
Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.

У кого можно попросить помощи, если очень трудно? (соседа по парте)

2+2		1+2		4-2
3+2		3-1		5-3

– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными. Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)

– Перед вами знаки. Как называется первый знак? (больше)

Как называется второй знак? (меньше)

Напишите знак по точкам, допишите до конца строки.

Учитель:
Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».

Карточка.

2*3		5*7		8*5
5*3		10*7		6*2
3*9		7*1		6*9

3. Рефлексия:

Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.

– Скажите, что вы для себя узнали нового?

– Чем мы сегодня занимались?

– Что вам помогло хорошо работать на уроке?

У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)

Полёт завершён, всем спасибо!

Внимание! Перед вами ознакомительная версия урока, материалы которого могут быть неполными. Войдите на сайт как ученик

Войдите на сайт как ученик

Войдите как ученик, чтобы получить доступ к материалам школы

Типы операторов

Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.

Для выполнения основных математических операций, таких как сложение, вычитание, умножение и объединение чисел, а также для получения числовых результатов используйте арифметические операторы в этой таблице.

Возведение в степень

С помощью операторов в приведенной ниже таблице вы можете сравнить два значения. При сравнении двух значений с помощью этих операторов результатом будет логическое значение либо истина, либо ложь.

= (знак «больше или равно»)

Больше или равно

С помощью амперсанда (&) можно присоединиться к одной или нескольким текстовым строкам или объединить их в виде одной части текста.

Соединение или сцепление двух значений для получения одного непрерывного текстового значения.

Объединение диапазонов ячеек для вычисления с помощью этих операторов.

Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки.

Оператор Union, объединяющий несколько ссылок в одну ссылку.

= СУММ (B5: B15, D5: D15)

Оператор пересечения, который создает ссылку на ячейки, которые являются общими для двух ссылок.

= СУММ (B7: D7 C6: C8)

Символ # используется в нескольких контекстах:

Используется в качестве части имени ошибки.

Используется для обозначения недостаточного места для отображения. В большинстве случаев вы можете расширить столбец, чтобы его содержимое отображалось правильно.

Заменяющий оператор Range, который используется для ссылки на весь диапазон в формуле динамического массива.

Оператор ссылки, который используется для указания неявного пересечения в формуле.

= СУММ (Таблица1 : ])

Голодная птичка

Для игры понадобится знак раскрытый клюв (знак больше). Его можно вырезать из картона или сделать большую модель из одноразовой тарелки. Чтобы заинтересовать малыша, можно приклеить или дорисовать глаза, перья, а рот сделать открывающимся.

После этого наглядно показывается, что птичка открывает клюв в сторону, где больше предметов.

Далее полученная информация закрепляется: на столе выкладываются кучки с зернышками, а ребенок определяет, в какую сторону птичка повернет свой клюв. Если не удастся правильно расположить его с первого раза, нужно помочь, еще раз проговорив, что рот открыт в сторону большего количества еды. Затем можно предложить еще несколько аналогичных заданий: числа написаны на листе, нужно правильно приклеить клюв.

Примеры можно разнообразить, заменив птичку щукой, крокодилом или любым другим хищником, который также разевает пасть в сторону большего числа.

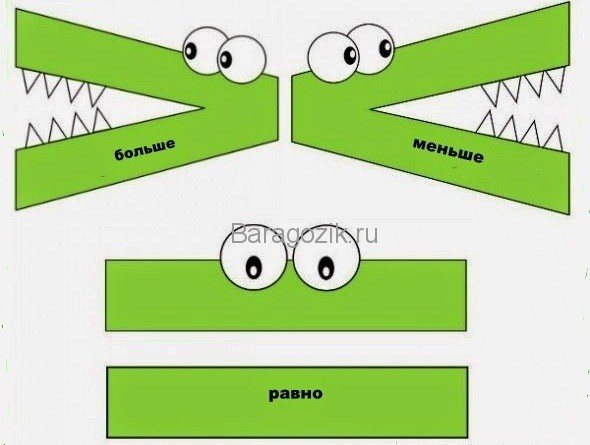
Могут попасться необычные ситуации, где количество предметов в обеих кучках будет равное. Если ребенок это заметит значит, внимательный.

За это нужно обязательно похвалить, а потом показать 2 одинаковые полоски и объяснить, что они такие же одинаковые, как и число предметов в кучках, а раз количество предметов равное, то и знак называется равно.

Что в приоритете знак или дорожная разметка на дороге по ПДД

Х

Таким образом в настоящее время практически все случаи противоречия дрожных знаков и разметки урегулированы Правилами дорожного движения.

Интересным является тот факт, что даже постоянный знак дорожного движения имеет приоритет над временной разметкой, т.е. действовавший раньше принцип главенства любых временных изменений над постоянными знаками и разметкой в некоторой степени не действует, что нужно иметь ввиду водителю.

Однако не все так радужно, казалось бы все случаи урегулировали, все вопросы должны быть сняты, но фактически следующая проблема осталась:

– противоречия между знаками или дорожными разметками одинакового статуса. Да-да, именно так, как показывает практика, нередко встречаются и ситуации, когда друг другу противоречат два постоянных знака, или два временных знака, или на асфальт нанесено несколько противоречивых разметок желтого цвета (старую еще не стерли, а сдвинулась область ремонта и нанесли новую).

Этот вопрос решается исходя из указания ГИБДД, текст которого приведен ниже в исторической справке.

ИСТОРИЧЕСКАЯ СПРАВКА

До выхода Постановления Правительства РФ от 10 мая 2010 г. N 316 в ПДД были описаны не все случаи противоречия знаков и разметки и таблца являлась неполной. Эти-то случаи как раз и представляли для нас наибольший интерес.

Не были описаны в ПДД два интереснейших случая, которые в результате и вызывали множество споров и судов:

– стационарный знак противоречит временной разметке;

– стационарный знак противоречит постоянной разметке.

Давайте рассмотрим ранее действовашие нормы в отношении этих двух случаев поподробнее.

Стационарный знак противоречит временной разметке.

Почему-то этот случай был незаслуженно обойден вниманием специалистов и отдан на откуп сотрудников ГИБДД. У обывателя бытует поверье, что в целях ПДД все временное имеет приоритет над постоянным и каждый автомобилист готов согласиться с сотрудником ДПС, что временная разметка имеет приоритет и над постоянной разметкой и над стационарными знаками

Но на самом-то деле, как мы могли убедиться выше, читая выдержки из ПДД, это всего лишь заблуждение, в ПДД не было таких разъяснений относительно противоречия временной разметки и стационарного знака, соответственно мы получали правовую коллизию, а все сомнения, как известно, толкуются в пользу обвиняемого.

«30 декабря 2001 года N 195-ФЗ

КОДЕКС РОССИЙСКОЙ ФЕДЕРАЦИИ

ОБ АДМИНИСТРАТИВНЫХ ПРАВОНАРУШЕНИЯХ

Статья 1.5. Презумпция невиновности

4. Неустранимые сомнения в виновности лица, привлекаемого к административной ответственности, толкуются в пользу этого лица».

Однако, как мы знаем, подобные декларативные нормы редко соблюдаются, и поэтому к разрешению данной ситуации мы еще вернемся ниже.

Стационарный знак противоречит постоянной разметке.

Этот случай, который в принципе возникать не должен, однако возникает в силу российской действительности, также никаоим образом не находил отражения в законодательстве. Однако в данном случае на помощь нам в 2008 году совершенно неожиданно пришло руководство ГИБДД, за что можно сказать большое спасибо, и пожелать и в дальнейшем работать так же четко и стоять на страже интересов водителей.

14.02.2021ovrautozona

Последние сообщения

• Как запомнить сигналы регулировщика ПДД10.04.2021
• Как проверить номер диагностической карты техосмотра10.04.2021
• Как узнать налоги на сайте госуслуги10.04.2021

Порядок выполнения действий в формулах Excel

В некоторых случаях порядок, в котором выполняется вычисление, может влиять на возвращаемое значение формулы, поэтому важно понимать порядок, а также изменять порядок получения результатов, которые вы ожидаете отобразить. Формулы вычисляют значения в определенном порядке

Формула в Excel всегда начинается со знака равенства (=). Знак равенства указывает на то, что Подпишитесь на формулу в Excel. После этого знака равенства можно вычислить ряд элементов (операндов), разделенных операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле

Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равенства (=). Знак равенства указывает на то, что Подпишитесь на формулу в Excel. После этого знака равенства можно вычислить ряд элементов (операндов), разделенных операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом — например, операторы деления и умножения, — они выполняются слева направо.

Возведение в степень

Умножение и деление

Сложение и вычитание

Объединение двух текстовых строк в одну

Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, следующая формула возвращает значение 11, так как Excel вычисляет умножение до сложения. Формула сначала умножает число 2 на 3, а затем добавляет 5 к результату.

Если вы используете скобки для изменения синтаксиса, Excel складывает 5 и 2, а затем умножает результат на 3, чтобы получить 21.

В приведенном ниже примере круглые скобки, которые заключаются в первой части формулы, заставляют Excel сначала вычисляют B4 + 25, а затем делят результат на сумму значений в ячейках D5, «5» и «F5».

Посмотрите это видео в порядке операторов в Excel , чтобы узнать больше.

Свойства неравенств

Опишем свойства неравенств. Очевидный факт, что объект никак не может быть неравным самому себе, и это есть первое свойство неравенства. Второе свойство звучит так: если первый объект не равен второму, то и второй не равен первому.

Опишем свойства, соответствующие знакам «больше» или «меньше»:

Определение 5

• антирефлективность. Это свойство можно выразить так: для любого объекта k неравенства k>k и k<k неверны;
• антисимметричность. Данное свойство говорит о том, что, если первый объект больше или меньше второго, то второй объект, соответственно, меньше или больше первого. Запишем: если m>n, то n<m. Или: если m<n, то n>m;
• транзитивность. В буквенной записи указанное свойство будет выглядеть так: если задано, что a<b и b<с, то a<c.  Наоборот: a>b и b>с, а значит a>c. Данное свойство интуитивно понятно и естественно: если первый объект больше второго, а второй – больше третьего, то становится ясно, что первый объект тем более больше третьего.

Знакам нестрогих неравенств также присущи некоторые свойства:

Определение 6

• рефлексивность: a≥a и a≤a (сюда же включается случай, когда a=a);
• антисимметричность: если a≤b, то b≥a. Если же a≥b, то b≤a;
• транзитивность: если a≤b и b≤c, то очевидно, что a≤c. И также: если а≥b, а b≥с, то а≥с.

Двойные неравенства, тройные неравенства и т. д.

Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.

Пример. Известно, что  4 < 7,  а  7 < 16.  Эти два неравенства удобнее представить в виде двойного неравенства:

4 < 7 < 16.

Двойные неравенства принято читать с середины. Например, неравенство  2 < 4 < 5  читается так: четыре больше двух, но меньше пяти.

В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.

Пример. Допустим, нужно сравнить три натуральных числа  11,  34  и  8.  Сравнивая данные числа между собой, получим три неравенства  11 < 34,  8 < 11  и  34 > 8,  которые можно записать как двойное неравенство:

8 < 11 < 34.

Аналогичным образом строятся тройные, четверные и т. д. неравенства.

Пример. Известно, что  12 < 15,  47 > 15,  47 < 112,  тогда можно записать

12 < 15 < 47 < 112.