Этап сетевого планирования проекта
Содержание:
- Построение сетевого графика
- Метод сетевой модели номер два
- Масштабный сетевой график
- Общие характеристики МКП
- Методы оптимизации сетевого графика
- Использование табличного метода
- Onlinecharts.ru
- Корректировка сетевой модели
- Что это?
- Минимизация числа исполнителей проекта при сохранении времени его выполнения
- Работа с расписанием в МКП
Построение сетевого графика
В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.
В таблицу сведем следующие данные по каждой операции:
- номер операции;
- предшествующие операции;
- количество исполнителей;
- продолжительность операции в днях.
В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.
|
Номер операции |
Предыдущие операции |
Кол-во исполнителей, чел. |
Продолжительность, дни |
|---|---|---|---|
|
1. |
— |
10 |
1 |
|
2. |
1 |
2 |
3 |
|
3. |
1 |
3 |
1 |
|
4. |
1 |
2 |
4 |
|
5. |
4 |
1 |
0,5 |
|
6. |
3 |
3 |
2 |
|
7. |
5 |
2 |
0,5 |
|
8. |
2,7,6 |
10 |
0,5 |
|
9. |
9 |
10 |
0,5 |
|
10. |
9 |
1 |
3 |
|
11. |
9 |
2 |
4 |
|
12. |
9 |
2 |
2 |
|
13. |
9 |
2 |
3 |
|
14. |
12 |
2 |
2 |
|
15. |
13 |
3 |
2 |
|
16. |
10,11,14,15 |
10 |
0,5 |
|
17. |
16 |
10 |
0,5 |
|
18. |
17 |
2 |
2 |
|
19. |
18 |
2 |
3 |
|
20. |
17 |
2 |
2 |
|
21. |
17 |
2 |
3 |
|
22. |
21 |
3 |
1 |
|
23. |
20 |
2 |
2 |
|
24. |
19,22,23 |
10 |
0,5 |
|
25. |
24 |
10 |
0,5 |
|
26. |
25 |
5 |
1 |
|
27. |
26 |
5 |
3 |
|
28. |
25 |
3 |
2 |
|
29. |
28 |
3 |
2 |
|
30. |
25 |
2 |
4 |
|
31. |
27,29,30 |
10 |
0,5 |
|
32. |
31 |
10 |
0,5 |
|
33. |
32 |
7 |
1 |
|
34. |
32 |
2 |
1 |
|
35. |
33,34 |
10 |
1 |
На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.
Сетевой график, пример
Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.
В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.
Для соблюдения запланированных сроков произведем корректировку сетевого графика.
В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.
После корректировки осуществим построение альтернативного сетевого графика.
Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:
Q = N * t
Q4 = 2*4 = 8 ч/дн
Q13 = 2*3 = 6 ч/дн
Q18 = 2*2 = 4 ч/дн
В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.
В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.
В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.
В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:
26 – 2 – 1 – 1 = 22 дня.
Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.
Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.
Альтернативный сетевой график
Метод сетевой модели номер два
Вторым методом сетевого планирования, по праву завоевавшим популярность среди проект-менеджеров, является диаграмма, называемая «вершина – работа». В англоязычной версии модель сокращенно обозначается как AoN (Activity on Node). Метод отличается большей простой и наглядностью, предлагает узлами модели делать не события, а работы. При этом длина прямоугольников, обозначающих операции, может указывать на их длительность во времени. Отношения предшествования между ними оформляются прямыми или фигурными стрелками.
Такую диаграмму сформировать значительно проще, чем AoA. Тем не менее, алгоритм работы над ней очень похож. События на диаграмме не размещаются, но они предполагаются в завершении каждой работы. Помимо прочего, событиям все-таки уготовано место на сетевом графике, но в форме особых фактов, именуемых вехами. Веха – это особенное значимое событие проекта, и не каждая операция должна ею завершаться. Поэтому диаграмма может быть разгружена от несущественных событий, но отражать важные, ключевые моменты проектной реализации.
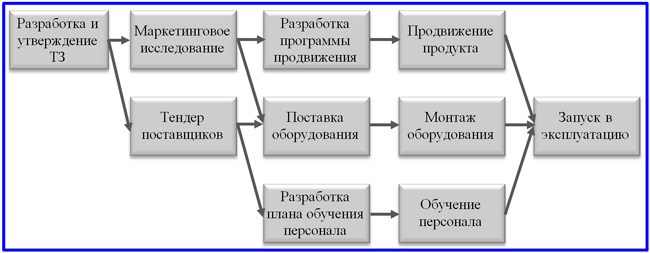 Пример сетевой диаграммы метода «вершина – работа»
Пример сетевой диаграммы метода «вершина – работа»
Если воспользоваться возможностью вариации длины прямоугольников работ, превращая их в ленты, размер которых соответствует длительности реализации, то сетевой график превращается в диаграмму Ганта. Диаграмма вида AoN при этом становится похожей на АоА. В методе AoN отпадает необходимость в изображении фиктивных работ, требуемых в модели «ребро – работа» для своеобразной «упаковки» событий. Благодаря этому лишние, искусственные сущности исключаются из поля зрения менеджера проекта. Вехи в этом отношении являются более интересным решением, располагаясь, как и все работы, в узлах сетевого графика.
Работы перестают выполнять двойную функцию связующих события элементов и непосредственного обозначения выполняемых операций. Для метода AoN не требуется нумерации, что дает PM мобильность для свободного маневрирования числом мероприятий. И в этом кроется еще одно удобство метода «вершина – работа». В сетевой диаграмме должны быть учтены возможности применения различных связей предшествования. Их количество не столь велико, как может показаться на первый взгляд. Оно связано с вариантом связи предшествования и с эффектом отставания или опережения в отношении к примененной типовой связи. Все это мы рассмотрим в отдельном материале, посвященном практике сетевого планирования и управления.
В настоящей статье мы рассмотрели методы сетевого планирования и управления. В современной проектной практике отдается предпочтение методу AoN как более доступному и наглядному. Это не означает, что метод АоА плох, многие специалисты, освоив его, с успехом применяют. Обе модели приводят к одному и тому же результату, но с двух взаимосвязанных сторон: работ и событий. Проект-менеджер должен понимать суть и уметь применять каждый из представленных инструментов. Это связано с тем, что задача сетевого планирования состоит в поиске наиболее экономичных, ясных решений построения событийной и временной последовательности в условиях ограничений.
Масштабный сетевой график
- Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
- Построить масштабный сетевой график.
- Оценить вероятность выполнения всего комплекса работ за 30 дней.
- Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
| Код работы ( i,j) | Продолжительность | |
| tmin (i,j) | tmax (i,j) | |
| 1,2 | 5 | 10 |
| 1,4 | 2 | 7 |
| 1,5 | 1 | 6 |
| 2,3 | 2 | 4,5 |
| 2,8 | 9 | 19 |
| 3,4 | 1 | 3,5 |
| 3,6 | 9 | 19 |
| 4,7 | 4 | 6,5 |
| 5,7 | 2 | 7 |
| 6,8 | 7 | 12 |
| 7,8 | 5 | 7,5 |
Решение находим с помощью сервиса Сетевая модель
. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная tmax(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение tож(i,j) оценивается по формуле
tож(i,j)=(3 tmin(i,j)+2 tmax (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(tmax(i,j)-tmin(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
tож(1,2)=(3*5+2*10)/5=7
tож(1,4)=(3*2+2*7)/5=4
tож(1,5)=(3*1+2*6)/5=3
tож(2,3)=(3*2+2*4,5)/5=3
tож(2,8)=(3*9+2*19)/5=13
tож(3,4)=(3*1+2*3,5)/5=2
tож(3,6)=(3*9+2*19)/5=13
tож(4,7)=(3*4+2*6,5)/5=5
tож(5,7)=(3*2+2*7)/5=4
tож(6,8)=(3*7+2*12)/5=9
tож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25
Полученные данные занесем в таблицу.
Таблица – Сетевая модель.
| Работа ( i,j) | Продолжительность | Ожидаемая продолжительность tож(i,j) | Дисперсия S2(i,j) | |
| tmin (i,j) | tmax (i,j) | |||
| 1,2 | 5 | 10 | 7 | 1 |
| 1,4 | 2 | 7 | 4 | 1 |
| 1,5 | 1 | 6 | 3 | 1 |
| 2,3 | 2 | 4,5 | 3 | 0,25 |
| 2,8 | 9 | 19 | 13 | 4 |
| 3,4 | 1 | 3,5 | 2 | 6,25 |
| 3,6 | 9 | 19 | 13 | 4 |
| 4,7 | 4 | 6,5 | 5 | 0,25 |
| 5,7 | 2 | 7 | 4 | 1 |
| 6,8 | 7 | 12 | 9 | 1 |
| 7,8 | 5 | 7,5 | 6 | 0,25 |
| КПР | Код работы (i,j) | Продолжительность работы t(i, j) | Ранние сроки | Поздние сроки | Резервы времени | |||
| tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rc | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1,2 | 7 | 7 | 7 | |||||
| 1,4 | 4 | 4 | 17 | 21 | 17 | 8 | ||
| 1,5 | 3 | 3 | 19 | 22 | 19 | |||
| 1 | 2,3 | 3 | 7 | 10 | 7 | 10 | ||
| 1 | 2,8 | 13 | 7 | 20 | 19 | 32 | 12 | 12 |
| 1 | 3,4 | 2 | 10 | 12 | 19 | 21 | 9 | |
| 1 | 3,6 | 13 | 10 | 23 | 10 | 23 | ||
| 2 | 4,7 | 5 | 12 | 17 | 21 | 26 | 9 | |
| 1 | 5,7 | 4 | 3 | 7 | 22 | 26 | 19 | 10 |
| 1 | 6,8 | 9 | 23 | 32 | 23 | 32 | ||
| 2 | 7,8 | 6 | 17 | 23 | 26 | 32 | 9 | 9 |
кр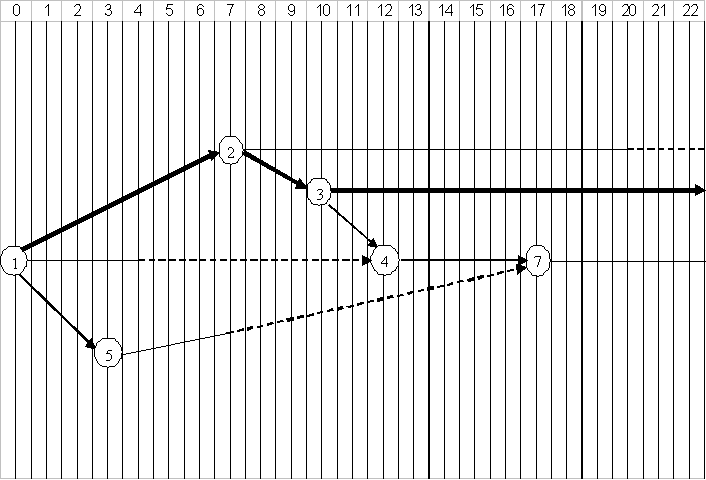
P(tкр
где Z=(Т-Ткр)/SкрZ- нормативное отклонение случайной величины, Sкр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.
| Z | F(Z) | Z | F(Z) | Z | F(Z) |
| 0.0000 | 1.0 | 0.6827 | 2.0 | 0.9643 | |
| 0.1 | 0.0797 | 1.1 | 0.7287 | 2.1 | 0.9722 |
| 0.2 | 0.1585 | 1.2 | 0.7699 | 2.2 | 0.9786 |
| 0.3 | 0.2358 | 1.3 | 0.8064 | 2.3 | 0.9836 |
| 0.4 | 0.3108 | 1.4 | 0.8385 | 2.4 | 0.9876 |
| 0.5 | 0.3829 | 1.5 | 0.8664 | 2.5 | 0.9907 |
| 0.6 | 0.4515 | 1.6 | 0.8904 | 2.6 | 0.9931 |
| 0.7 | 0.5161 | 1.7 | 0.9104 | 2.7 | 0.9949 |
| 0.8 | 0.5763 | 1.8 | 0.9281 | 2.8 | 0.9963 |
| 0.9 | 0.6319 | 1.9 | 0.9545 | 2.9 | 0.9973 |
Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S2(Lкр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(Lкр)=2,5
p(tкр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:
Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.
Общие характеристики МКП
Метод критического пути (МКП) – это способ, применяемый для нахождения минимальной продолжительности мероприятия, достижения допустимой гибкости в рамках логики календарной модели. Критический путь проекта может быть рассмотрен применительно к табличной форме представления расписания, использован для анализа диаграммы Ганта (линейной диаграммы) или в отношении сетевого графика. Поскольку метод обладает свойством визуальной наглядности, наибольшее применение он находит для оптимизации сетевого графика. МКП формулирует ряд требований к календарной модели.
- Все работы к моменту применения метода должны быть определены, их число, содержание должны быть точно установлены.
- Известна предполагаемая длительность выполнения каждой операции.
- Основным видом взаимосвязи между операциями является отношение предшествования, то есть начало последующей работы формируется в связи с окончанием предыдущей.
Критический путь представляет собой совокупность последовательно выполняемых операций, которая характеризуется максимальной продолжительностью из всех возможных путей в расписании. На данном пути общие временные резервы отсутствуют. Любые работы, лежащие на нем, называются операциями критического пути. В условиях сетевого графика может быть рассмотрено несколько параллельно намеченных последовательностей для целей нахождения резервов оптимизации календарной модели.
Расчет критического пути выполняется для целей:
- минимизации общей продолжительности мероприятия в условиях ограничений по срокам работ;
- ранжирования операций в любой момент реализации проекта в условиях решения общей задачи мероприятия в минимальные сроки;
- информирования PM об ограничивающем факторе критического пути, чтобы оптимизировать операции, влияющие на общую планируемую продолжительность.
Иными словами, анализ на основе МКП показывает, какие задачи и соответствующие им работы влияют на срок окончания проекта. Он позволяет менеджеру принять взвешенные решения по сжатию расписания. Анализ параметров операций сетевого графика дает возможность найти резервы некритических задач и использовать их при выравнивании загрузки ресурсов, используя следующий алгоритм МКП.
- Прямой анализ последовательностей работ, вычисление ранних начал и окончаний операций.
- Обратный анализ последовательностей, расчет поздних окончаний и поздних начал выполнения работ.
- Вычисление временных резервов для каждой из работ сетевого графика.
- Формирование плана мероприятий по оптимизации расписания.
Методы оптимизации сетевого графика
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.
Функционально-процессная блок-схема управления проектом
На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.
При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:
- для моделей с дискретным и непрерывным временем;
- для моделей с простым отношением предшествования;
- в сетях с обобщенными связями.
Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.
Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.
Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия
Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.
Модель расчета параметров сетевого графика табличным способом
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
- Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
- Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
- Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
- Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.
- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
Корректировка сетевой модели
Корректировка сетевой модели может проводиться и в первом случае, если имеется возможность для повышения эффективности реализации запланированных операций.
В сетевом планировании выделяют три способа корректировки модели:
- изменение сроков выполнения критических операций за счет привлечения дополнительных ресурсов, в качестве которых могут выступать денежные средства, материалы или человеческие ресурсы;
- изменение сроков выполнения критических операций за счет привлечения исполнителей, занятых на других операциях, при сохранении изначальных параметров ресурсов;
- изменение сроков выполнения операций за счет совмещения их выполнения.
В первом случае корректировка сетевой модели осуществляется без изменения сетевой диаграммы. Данный подход чаще всего практикуется в тех случаях, когда для выполнения операций остаются свободные ресурсы, не задействованные в других операциях.
Во втором случае сетевая диаграмма также остается неизменной. Данный подход используется в тех случаях, когда возможно увеличить срок выполнения операций, не принадлежащих к критическому пути.
Третий случай применяется при невозможности использования дополнительных ресурсов и подразумевает повторное построение сетевой диаграммы.
После проведения корректировки осуществляется построение альтернативной сетевой модели.
Следует отметить, что в корректировке сетевой модели заключается фундаментальное назначение сетевого планирования. Благодаря построению сетевых моделей уже на ранней стадии планирования могут быть выявлены условия, свидетельствующие о том, что в заданные директивные сроки проект невозможно будет выполнить. Поэтому для получения приемлемых с точки зрения целей проекта сроков возможно осуществление коррекции расписания операций по принципу изменения продолжительности критических операций. Таким образом, если проект или заданный план действий не укладывается в директивные сроки, то предпринимается попытка сократить сроки выполнения критических операций за счет изменения их зависимости от первоначально заданных параметров их выполнения.
Литература
- Черняк В.З., Довдиенко И.В. Методы принятия управленческих решений. – М.: Академия, 2013.
- Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г., Полковников А.В. Управление проектами. – М.: Омега-Л, 2012.
- Новыш Б.В., Шешолко В.К., Шаститко Д.В. Экономико-математические методы принятия решений. – М.: Инфра-М, 2013.
- Урубков А.Р., Федотов И.В. Методы и модели оптимизации управленческих решений. – М.: изд-во АНХ, 2011.
- Сухачев К.А., Колосова Е.С. Практика применения технологий календарно-сетевого планирования. // Нефтегазовая вертикаль. – 2010. – №11 (240), июнь 2010. – С. 28-30.
Что это?
Одной из методик эффективного планирования деятельности производственного предприятия является построение сетевого графика. Изначально он использовался в строительстве и определял не столько последовательность работ, сколько сроки выхода на строительную площадку бригад рабочих разных специальностей. Он называется «календарный план выполнения работ».
В современных условиях, когда крупные предприятия массово выпускают продукцию, для облегчения и повышения производительности весь процесс разбивается на простые операции. Поэтому сетевой график «перекочевал» из строительства практически во все отрасли.
Итак, что же отображается в этом документе? Во-первых, подробнейшим образом перечисляются все операции, необходимые для выпуска товаров (производства услуг). Во-вторых, определяется логическая взаимозависимость между ними. И, наконец, в-третьих, рассчитываются не только сроки выполнения каждой конкретной работы, но и время, необходимое для полного завершения производственного процесса.
Раскрывая внутренние зависимости операций проекта, сетевой график становится базой для календарного планирования загруженности оборудования и рабочей силы.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
линейная диаграммакарта проекта
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
калькулятора
Таблица 1
| Работа (ij) | Длительность t(ij), дн. | Количество исполнителей |
| 1,2 | 4 | 5 |
| 2,3 | 6 | 3 |
| 2,4 | 5 | 6 |
| 2,7 | 11 | 6 |
| 3,5 | 9 | 1 |
| 4,6 | 9 | 2 |
| 5,7 | 11 | 3 |
| 6,7 | 10 | 5 |
| 7,8 | 4 | 6 |
Рис. 1. Пример сетевого графика
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.
Видеоинструкция
Работа с расписанием в МКП
Этапы алгоритма МКП с 1-го по 3-й достаточно подробно изложены в статье на тему практики построения сетевого графика. Ниже мною приведен пример фрагмента модели, на которой критический путь показан стрелочками красного цвета. Его определить достаточно просто. Двигаться следует от конечной работы к начальной. Необходимо выбирать из всех предыдущих действий операцию, имеющую самое позднее раннее окончание. Именно такие операции будут лежать на критическом пути. Его нахождение можно выполнить и в табличной форме, пример применения МКП также приведен в указанном выше материале.
Пример фрагмента сетевого графика с выделенным критическим путем
В практике оптимизации календарных моделей действуют два иногда конкурирующих между собой ориентира: критический путь и загруженность временных ресурсов. На стыке интересов сохранения или уменьшения общего срока, с одной стороны, и достаточности ресурсов, с другой, строится деятельность по моделированию календаря. Среди способов действий в зоне взаимодействия данных интересов выделяются два: сглаживание ресурсов и их выравнивание.
Первый метод позволяет выполнить анализ и оптимизировать ресурсы, не заходя за рамки имеющихся резервов на выполнение задач мероприятия, и критический путь остается неизменным. При выравнивании РМ получает возможность изменения сроков работ, включая и операции критического пути. Это приводит к изменению сроков всего проекта. Все зависит от доминирования того или иного критерия среди сроков и ресурсного обеспечения. Ниже на схеме приведен перечень методов, которые руководитель может использовать для оптимизации модели.
Способы оптимизации модели календарного планирования
При проведении ресурсной оптимизации следует руководствоваться несколькими правилами:
- итерационно обращаться к методологии по мере надобности в течение всего периода реализации инвестиционного мероприятия;
- каждое действие следует наделять ресурсом с учетом его стоимости;
- не допускать длительной перегрузки ресурсов;
- учитывать уровень дискретности выполнения операций;
- выполнять анализ доступности ресурсов на основе календарей их загрузки;
- для выравнивания ресурсов использовать матрицу приоритета задач.
Что РМ может предпринять, если он не укладывается в установленные ему свыше сроки выполнения основной задачи, при этом ресурсные резервы еще не исчерпаны? Менеджер может выполнить сжатие календарного плана путем интенсификации работ, их распараллеливания или использовать комбинированный метод. Интенсификация применяется к работам, находящимся на критическом пути. Операции планируется выполнить быстрее, но при этом возрастает риск увеличения их стоимости за счет ресурсного насыщения. Второй способ предполагает сдвиг последующей операции на более ранние сроки, что дает эффект общего сокращения работ за счет параллельного выполнения. При этом возникает опасность, что работу придется переделывать.
МКП входит в состав базовых компетенций современного руководителя. Обладая видением критических задач, PM способен принимать более взвешенные решения по возможностям изменения графика, урезания несущественных действий и оптимизации ресурсов. Процедуры эти в рамках процессов планирования носят итеративный характер и позволяют построить оптимизированное, но вполне реалистичное расписание проекта.