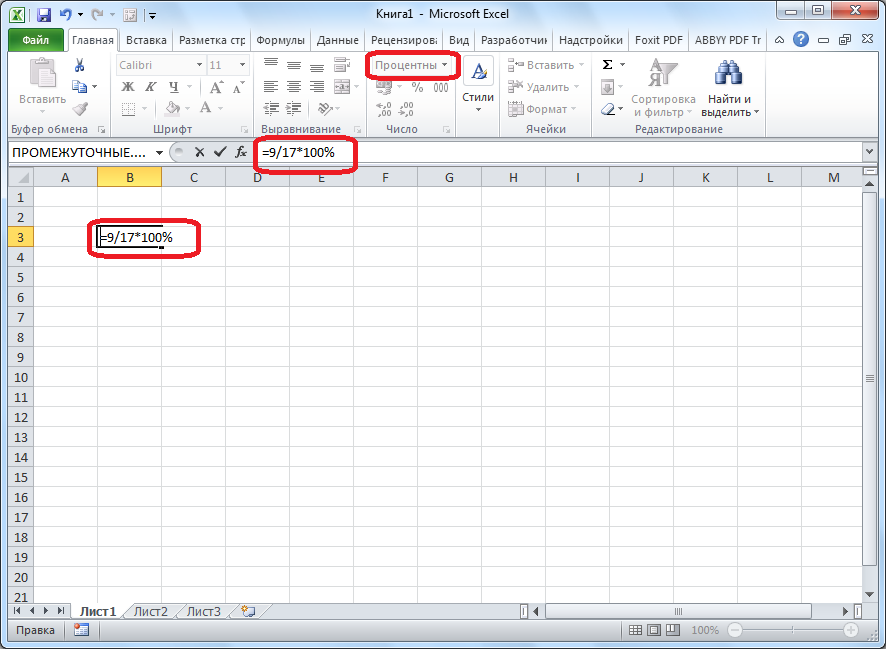
Как найти процент от числа? формула с примерами

Формулы для определения необходимой доли от суммы

Есть несколько способов найти требуемый процент от любого числа.

Первый способ состоит в делении нужной суммы на 100, после чего полученный результат умножается на % который необходимо определить.

Формула расчёта в данном случае выглядит так:

A / 100 * B =

В данной формуле A – это базовое число, из которого нужно извлечь долю.

B – процент, который необходимо высчитать в числовом выражении.

Например, в каком-либо магазине вам отдают товар, цена которого 500 рублей, за 70% его стоимости. Используя приведённую выше формулу, высчитываем, сколько нам необходимо заплатить в конечном итоге (или сколько будет 70% от 500 рублей):

500 / 100 * 70 = 350 рублей

Таким образом, мы сможем приобрести нужный товар за 350 рублей.

Второй способ состоит в умножении базового числа A на коофициент 0,B

Где А – это базовое число, а B – количество процентов, которые необходимо определить.

Формула имеет следующую форму:

A * 0,B =

В случае упомянутого выше примера с 70% стоимости от 500 высчитываем стоимость товара:

500 * 0,70 = 350

Третий способ состоит в умножении базового числа на количество процентов, после чего полученный результат делим на 100.

Формула выглядит следующим образом:

A * B  / 100 =

В нашем случае это:

500 * 70 / 100 = 350

На калькуляторе нужная доля от числа находится ещё проще:

1. Набираете на калькуляторе базовое число (А).
2. Жмёте на умножить, вводите искомое число процентов.
3. После чего жмёте на кнопку %, а затем на кнопку =. Калькулятор тот час же отобразит требуемый результат.

500*70% = (результат)

Насколько число меньше другого в процентах

К примеру: обычная стоимость порошка – 500 рублей. По акции, цену снизили до 480 рублей. Насколько цена по акции, меньше первоначальной в процентах? Вначале находят процентную составляющую акционной цены от базовой, а затем находиться их разница. Составляем пропорцию:

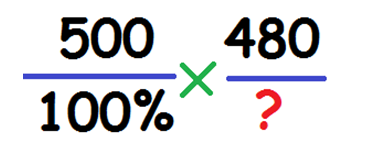
Вычисляем по формуле: (480*100)/500=96. 100%-96%=4%. Цена по акции меньше первоначальной на 4%.

Насколько число больше другого в процентах. Пример: клавиатура стоила 300 рублей, а после повышения курса доллара, цена выросла до 390 рублей. Насколько изменилась цена на клавиатуру в процентах? Вначале находиться общая процентная ставка новой цены, относительно первоначальной, затем вычисляется их разница. Составляем пропорцию:

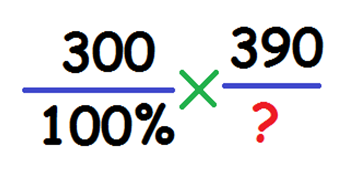
Вычисляем по формуле: (390*100)/300=130. 130%-100%=30%. Цена выросла на 30%.

Неизвестное число больше известного на определенный процент. Пример: товар в магазине, дороже товара на складе на 15%.  Цена сахара на складе – 50 рублей и приравнивается к 100%. Магазинная цена  – 100%+15%=115%. Вычисляем по формуле: (115*50)/100=57,5

Неизвестное число меньше известного на заданный процент. Пример: оптом на 5% дешевле. Цена за розницу – 60 рублей и равна 100 процентам, за опт – 100%-5%=95%. Составляем пропорцию:

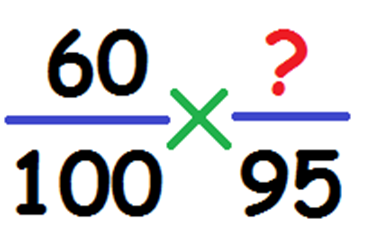
Вычисляем по формуле: (60*95)/100=57

Процент между двумя числами. Ситуация, когда известно число, составляющее 100% и число, составляющее некую долю от первоначального. Пример: ожидалась партия в 60 коробок, а завезли 53. На сколько процентов выполнился план. Составляем пропорцию:

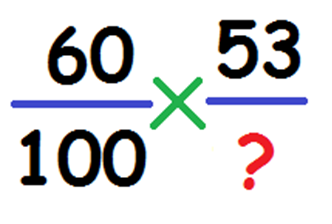
Вычисляем по формуле: (53*100)/60=88,3

Самая сложная «задача» — не запутаться в составлении пропорции.

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент. А что означает дробь одна сотая ? Эта дробь означает, что чего-либо разделено на сто частей и оттуда взята одна часть. Значит процентом является одна сотая часть чего-либо.

Процентом называется одна сотая часть чего-либо

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Как найти базовую сумму исходя из ее процента

В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?

Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:

67 / B * 100 = A

Подставляем значения:

67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)

Проверяем полученный результат с помощью формулы из первого способа:

293, 31 / 100 * 23 = 67

Всё сошлось.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Онлайн калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета % от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть %: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

5 класс, урок в самом разгаре, нужно определить процент от числа как можно быстрее — поможет онлайн калькулятор. Составлять расчет быстро и точно:

• Раз
• Два
• Три
• Четыре

Но помните, что на контрольных работах и экзаменах за вас никто не решит, а калькулятор не поможет.

Приходите практиковаться! В детской школе Skysmart ученики разбирают интересные задания, проходят квесты, играют в английский на интерактивной платформе и обсуждают темы, которые им интересны. Никаких скучных упражнений — только то, что зажигает вашего ребенка. Запишите его на бесплатный вводный урок и покажите, что английский может быть увлекательным путешествием!

Как рассчитать процент от суммы с помощью известных соотношений

Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т. д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.

Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.

Другими примерами таких соотношений будут:

• 12,5% — 1/8, то есть нужно делить на 8;
• 20% — 1/5, то есть нужно разделить на 5;
• 25% — 1/4, то есть делим на 4;
• 50% — 1/2, то есть нужно разделить пополам;
• 75% — 3/4, то есть нужно разделить на 4 и умножить на 3.

Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги,
2. доли в бизнесе,
3. доходность от инвестиций,
4. премии и штрафы,
5. инфляция.

И не только финансовые:

1. рождаемость и смертность,
2. статистика удачных и неудачных браков,
3. коэффициент полезного действия.

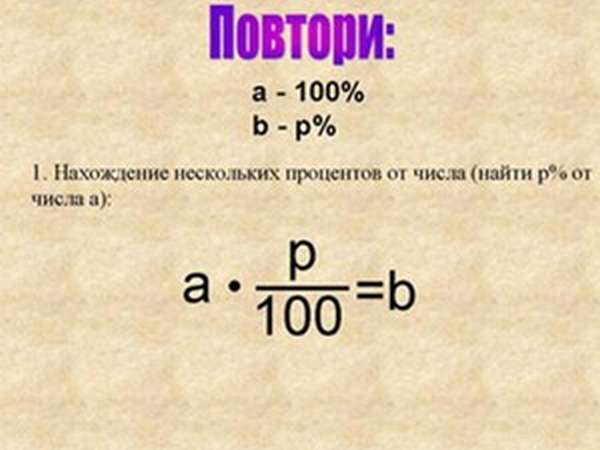Давайте разберёмся более подробно, как посчитать процент от суммы. Мы приведём вам несколько примеров, которые помогут вам все понять.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей,
2. мойку автомобиля — 250 рублей,
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Хитрости при нахождении процентов

Самый простой способ быстро все подсчитать — воспользоваться онлайн-калькулятором. У этого калькулятора очень простой интерфейс:

1. поле для введения процента,
2. поле для введения числа, процент от которого мы будем находить,
3. кнопка «Вычислить».

Вы можете легко найти такой калькулятор в интернете, вам не придётся заморачиваться с подсчётами. В принципе, это логично пользоваться всеми благами интернета. Однако в жизни бывают ситуации, когда необходимо посчитать процент от числа, но калькулятора под рукой нет.

Онлайн-калькуляторы вы можете найти на следующих сайтах:

1. calculator888.ru,
2. fin-calc.org.ua,
3. calc.by.

Если вам необходимо найти 20 или 40%, умножьте сумму на 0,2 и 0,4 соответственно.

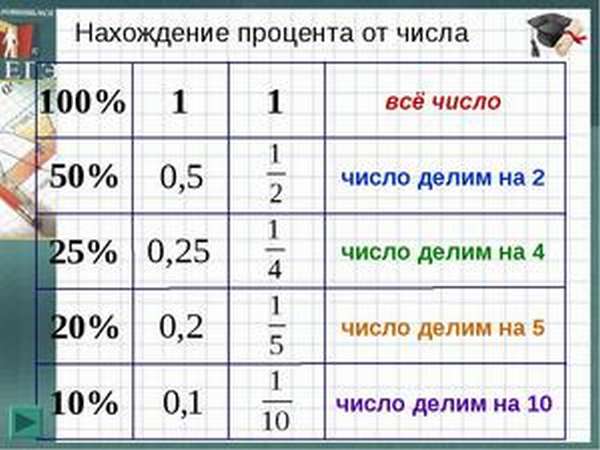
Очень простая техника нахождения процентов — деление. Но её можно использовать только с числами, на которые легко делится 100. Например, 100 легко делится на 25. Результат деления — четвёрка. Это значит, что для нахождения 25% от суммы необходимо просто разделить её на 4. По такой же схеме можно найти 10, 20 и 50% от нужной вам суммы.

Конечно же, необязательно считать в уме всё, вы можете разделить все на калькуляторе. Главное, что вы понимаете, как работает эта схема, и сможете легко применить её на практике.

Знание того, как посчитать проценты от процентов поможет вам планировать ваши доходы. Например, при депозитном вкладе с процентной ставкой 10% в год ваш доход за 2 года составит 21%. Потому что во втором году проценты начислялись уже на сумму, накопленную в течение первого года. А это 110% от суммы первоначального взноса.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Как вычислить на сколько процентов увеличилась или уменьшилась сумма

Это можно сделать способом, указанным в первом пункте способом: вычислить, сколько составляет 1%, затем получить разницу между данными (вычитать большую цифру из меньшей) и поделить ее на результат.

Пример: нужно вычислить, на сколько уменьшилось 200, если оно стало 150.

1. 200 – это 100%, 1% = 200/100 = 2.
2. 200-150 = 50.
3. 50/2 = 25, то есть 150 увеличилось на 25%.

Если необходимо посчитать, на сколько увеличилось, потребуется слегка изменить вычисления:

1. 150 – это 100%, то есть 1% =150/100 = 1,5.
2. 200-150 = 50.
3. 50/1,5 = 33,3%.

Стоит учесть: поскольку в первом случае цифра уменьшалась, а во втором – увеличилась, результаты тоже получились разными.

Чтобы вычислить отношение между увеличивающимися цифрами, можно воспользоваться еще одним способом. Для этого итоговое значение нужно разделить на начальное и посмотреть на три цифры после запятой. Переписав их отдельно и поставив запятую после первых двух, получим результат.

Лучше всего принцип действия виден на примере: нужно отыскать, на сколько увеличилась цифра, если из 150 она превратилась в 200.

1. 200/150 = 1,33333…
2. Три знака после запятой – это «333». Отделив первые две цифры, получим «33,3%».

Пример 2: из 100 получилось 110.

1. 110/100 = 1,1 или 1,100.
2. 100 – это 10,0%.

Вычисление процентов может потребоваться при разных подсчетах: для определения суммы налога, кредита, чтобы рассчитаться с клиентами по счету и т.д. Провести вычисления можно разными способами, выбрав наиболее понятный и простой.

Смотрите видео, в котором объясняется, как оперативно высчитать процент от суммы без калькулятора:

Рассчитываем сумму процентов кредита по ежемесячному дифференцированному платежу

Если Вы решились произвести расчёт процентов по кредиту, рекомендуем использовать калькулятор кредита онлайн с процентами, в котором достаточно указать все запрашиваемые данные. Собственными силами посчитать ставку и процент будет немного сложнее. Так, посчитанные платежи включают в себя следующие составляющие:

• Точно рассчитанная сумма, которую установил банк, начисленная для погашения кредита равными частями (перевод средств осуществляется каждый месяц).
• Процентная сумма, начисленная на кредитный остаток, то есть постоянно уменьшающаяся (при благоприятном раскладе) часть.

Чтобы установить точную сумму постоянного платежа, банковские сотрудники делят взятые в кредит средства на количество месяцев, в течение которых должно произойти погашение. Рассчитать проценты по кредиту позволяет довольно простая формула. Выглядит она так:

• Процентная сумма = (ООЗхПСхКДМ) / (100х365)
• Расшифруем составляющие формулы:
• ООЗ – остаток от основного займа.
• ПС – процентная ставка.
• КДМ – количество дней в месяце.

Вторая часть формулы – это произведение ста процентов на число дней в году.

В принципе, вычислить уровень переплаты по дифференцированной формуле несложно. Но если Вы хотите сэкономить собственное время, рациональнее использовать кредитный калькулятор в режиме онлайн. Программой всё рассчитывается по идентичной формуле, при этом итоговое значение окажется более точным.

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

Найти    от 10 см

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби 

Получили 0,1. Теперь 0,1 умножаем на числитель дроби 

0,1 × 2 = 0,2

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

0,2 см = 2 мм

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

300 : 100 = 3

Теперь полученный результат умножаем на 50

3 × 50 = 150 руб.

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

Например, те же 50% можно заменить на запись  . Тогда задание будет выглядеть так: Найти  от 300 рублей, а решать такие задачи для нас пока проще

300 : 100 = 3

3 × 50 = 150

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

1200 : 100 = 12

12 × 32 = 384

Ответ: 384 костюмов нового фасона выпустила фабрика.

Как найти процент от числа. Варианты

Рассмотрим по порядку ситуации по нахождению процентов.

Как найти 100%. Необходимо вычислить число, 15% от которого равно 45. Составляем пропорцию:

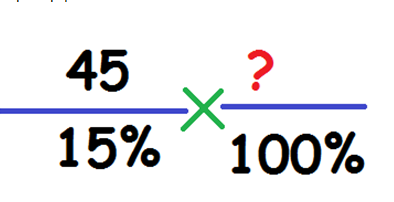
Вычисляем по формуле: (45*100)/15=300

Если не известно, сколько составляет 100%. Иногда расчет проводиться относительно одних и тех же первоначальных данных, но неизвестно их точное значение. К примеру: вчера продали 15% от общего количества печенья на сумму 450 рублей, а сегодня 25%.

На какую сумму продали сегодня? Так как сумма за 100% является общей величиной и для 15% и для 25%, можно проводить вычисления без поиска полной стоимости.

Вычисляем по формуле: (25*450)/15=750

Можно усложнить задачу, если нет уверенности в расчетах, или возникла потребность проверить результат. Для этого, вначале находиться 100%, на основе полноценных данных (15% стоит 450 рублей), а затем от 100% отсчитывают 25%.

Расчет при помощи пропорций

Этот способ высчитывания известен всем со школьной программы.

Расчет применяют в случаях, когда необходимо высчитывать процентное соотношение между двумя данными. Иначе говоря, если одно число представляет собой 100%, то сколько будет составлять второе?

Например, Х (икс) – это 100%, Y – это n%. Для вычисления значения n необходимо записать пример в следующем виде:

X = 100.

Y = n.

Перемножив числа по диагоналям, получим пропорцию:

X*n = Y*100.

n = (Y*100)/X.

Пример.

Нужно посчитать, какую долю от 500 составят 25.

1. 500 = 100%, 25 = n%.
2. n = (25*100)/500 = 5%.

Обратите внимание: в этих случаях Y должно быть меньше Х, иначе результат получится больше 100%.

Если нужно получить число, которое составляет какую-либо часть, потребуется воспользоваться обратной формулой:

Y = (n*X)/100.

Пример.

Нужно подсчитать, сколько будет 5% от 500.

Y = (5*500)/100 = 25.

Составляем пропорцию

Пропорции нас учили составлять еще в школе. На мой взгляд, это самый удобный способ считать проценты. Как гласит математическое правило, произведение крайних членов пропорции равно произведению её средних членов.

Разберемся на примере.

Вы решили приготовить пасту и купили сыр и томатную пасту. Но, вместо кусочка сыра 150 грамм, перепутали и взяли 120. Теперь вам нужно рассчитать, сколько томатной пасты нужно положить в блюдо.

Вычислим процентную долю сыра.

150гр: 100% = 120 гр : Х, где Х масса вашего кусочка сыра.

Х = 120 × 100 / 150 = 80%

Теперь составляем пропорцию, чтобы выяснить, сколько томатной пасты нам нужно:

150 г.: 100% = Х : 80%, где Х — нужное количество масла.

Х = 80 × 150 / 100 = 120

Получается, что для пасты вам потребуется 120гр. томатов.

Пример расчета скидки

Чтобы рассчитать насколько выгодна скидка, также подойдет формула пропорций. Например, вещь стоит 2499, а скидка на нее 15%.

Узнаем цену в процентах. Для этого отнимаем 15 от 100 = 85%.

Составляем пропорцию. 2499 : 100 = Х : 85

Х = 85 × 2499 / 100

Х = 2124, 15

Не слишком выгодная цена для вещи, которую вы так долго ждали. Может быть в следующем месяце магазин даст более выгодную цену?