1000 цифр числа пи в python

Сумма в питоне и разность в питоне

В Python операторы суммы и разности выполняют те же операции, что и в математике. Поэтому вы можете использовать этот язык программирования как калькулятор.

Рассмотрим некоторые примеры. Начнём с целых чисел:

print(1 + 5)

Вывод

6

Вместо передачи целых чисел напрямую в функцию  мы можем инициализировать переменные для этих значений:

a = 88
b = 103
print(a + b)

Вывод

191

Целые числа могут быть как положительными, так и отрицательными. Поэтому можно добавлять отрицательные числа к положительным:

c = -36
d = 25
print(c + d)

Вывод

-11

Прибавление работает аналогично и с числами с плавающей запятой:

e = 5.5
f = 2.5
print(e + f)

Вывод

8.0

Синтаксис разности тот же, что и для прибавления, за исключением того, что вместо оператора сложения () необходимо использовать оператор вычитания ():

g = 75.67
h = 32
print(g - h)

Вывод

43.67

В этом примере мы вычитаем целое число из числа с плавающей точкой. Python возвратит число с плавающей точкой, если хотя бы одно из чисел выражения является числом с плавающей точкой.

Полярные и прямоугольные координаты

Мы можем записать комплексное число в полярных координатах, которое представляет собой набор модуля и фазы комплексного числа.

Мы можем использовать функцию cmath.rect(), чтобы создать комплексное число в прямоугольном формате, передав модуль и фазу в качестве аргументов.

c = 1 + 2j

modulus = abs(c)
phase = cmath.phase(c)
polar = cmath.polar(c)

print('Modulus =', modulus)
print('Phase =', phase)
print('Polar Coordinates =', polar)

print('Rectangular Coordinates =', cmath.rect(modulus, phase))

Вывод:

Modulus = 2.23606797749979
Phase = 1.1071487177940904
Polar Coordinates = (2.23606797749979, 1.1071487177940904)
Rectangular Coordinates = (1.0000000000000002+2j)

Для чего нужен модуль Decimal?

Некоторые пользователи задаются вопросом, зачем нам нужен модуль для выполнения простейшей арифметики с десятичными числами, когда мы вполне можем сделать то же самое с помощью чисел с плавающей точкой ?

Перед тем, как мы ответим на данный вопрос, мы хотим, чтобы вы сами посчитали в Python, какой результат будет в данном примере: 0.1+0.2? Вы будете удивлены, когда узнаете, что правильный ответ – это не 0,3, а 0,30000000000000004.

Чтобы понять, почему в расчетах возникла ошибка, попробуйте представить 1/3 в десятичной форме. Тогда вы заметите, что число на самом деле не заканчивается в базе 10. Так как все числа должны быть каким-то образом представлены, при их сохранении в консоли делается несколько приближений, что и приводит к ошибкам.

Cпециально для читателей-гуманитариев, у нас есть объяснение принципов работы модулей Питона: «Она на долю секунды отвела взгляд» и «Она отвела взгляд на короткое время» — чувствуете разницу?

Чтобы получить точные результаты, подобные тем, к которым мы привыкли при выполнении расчетов вручную, нам нужно что-то, что поддерживает быструю, точно округленную, десятичную арифметику с плавающей запятой, и модуль Decimal отлично справляется с этой задачей. Теперь, когда мы разобрались с теорией, переходим к принципам работы десятичного модуля.

Тригонометрические функции

Тригонометрические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Sine:', cmath.sin(a))
print('Cosine:', cmath.cos(a))
print('Tangent:', cmath.tan(a))

print('ArcSin:', cmath.asin(a))
print('ArcCosine:', cmath.acos(a))
print('ArcTan:', cmath.atan(a))

Вывод:

Sine: (3.853738037919377-27.016813258003936j)
Cosine: (-27.034945603074224-3.8511533348117775j)
Tangent: (-0.0001873462046294784+0.999355987381473j)
ArcSin: (0.6339838656391766+2.305509031243477j)
ArcCosine: (0.9368124611557198-2.305509031243477j)
ArcTan: (1.4483069952314644+0.15899719167999918j)

Как отфильтровать элементы с помощью takewhile() и drop while()

Мы можем использовать Python для фильтрации элементов последовательности, если условие . Если условие становится , фильтрация прекращается.

iterator = itertools.takewhile(condition, *sequence)

Вот простой пример, который фильтрует числа, если число положительное.

import itertools

sequence = itertools.takewhile(lambda x: x > 0, )

for item in sequence:
    print(item)

Выход

1
2
3

Здесь последовательность остановилась после 3, поскольку следующий элемент равен -1.

Точно так же фильтрует элементы, пока условие имеет значение и возвращает все элементы после первого значения, отличного от false.

import itertools

data = itertools.dropwhile(lambda x: x < 5, )
for item in data:
    print(item)

Выход

12
7
1
-5

Константы и специальные значения

math.pi

Возвращает значение математической константы \(\pi\) с точностью, которая зависит от конкретной платформы.

math.e

Возвращает значение математической константы \(e\) с точностью, которая зависит от конкретной платформы.

math.inf

Возвращает положительную бесконечность, значение которое является типом float и может присутствовать в математических выражениях.

Данное значение можно получить с помощью команды . А что бы получить отрицательную бесконечность достаточно добавить перед командой унарный оператор :

Доступно в Python начиная с версии 3.5.

math.nan

Возвращает значение «не число» которое является типом float и может присутствовать в математических выражениях. Равносильно команде .

Доступно в Python начиная с версии 3.5.

math.isinf(x)

Возвращает True в случаях, когда x является отрицательной или положительной бесконечностью, иначе возвращает False.

math.isnan(x)

Возвращает True если x является nan, иначе возвращает False.

math.isfinite(x)

Возвращает False если x является либо nan, либо inf или -inf, во всех остальных случаях возвращается True.

Операторы сравнения

Оператор
Пример
Смысл
Результат

Эквивалентно

если значение равно значению , в противном случае

Не эквивалентно

если не равно и в противном случае

Меньше

если меньше чем , в противном случае

Меньше или равно

если меньше или равно , в противном случае

Больше

если больше , в противном случае

Больше или равно

если больше или равно , в противном случае

Вот примеры используемых операторов сравнения:

>>> a = 10
>>> b = 20
>>> a == b
False
>>> a != b
True
>>> a <= b
True
>>> a >= b
False
>>> a = 30
>>> b = 30
>>> a == b
True
>>> a <= b
True
>>> a >= b
True

Операторы сравнения обычно используются в булевых контекстах, таких как условные операторы и операторы цикла, для процессом вычислений, как вы увидите позже.

Равенство для значений с плавающей точкой

Вспомните из более раннего обсуждения , что значение хранится внутри для объекта может быть не совсем таким, как вы думаете. По этой причине не рекомендуется сравнивать значения с плавающей точкой для точного равенства. Рассмотрим этот пример:

>>> x = 1.1 + 2.2
>>> x == 3.3
False

Бабах! Внутренние представления операндов сложения не совсем равны и , поэтому вы не можете полагаться на для точного сравнения с .

Предпочтительным способом определения того, являются ли два значения с плавающей точкой «равными», является вычисление того, находятся ли они близко друг к другу, с учетом некоторого допуска. Посмотрите на этот пример:

>>> tolerance = 0.00001
>>> x = 1.1 + 2.2
>>> abs(x - 3.3) < tolerance
True

Функция возвращает абсолютное значение. Если абсолютное значение разности между двумя числами меньше указанного допуска, они достаточно близки друг к другу, чтобы считаться равными.

Арифметические функции в Python

Арифметические функции используются для представления чисел в различных формах и осуществления над ними математических операций. Далее представлен перечень самых популярных арифметических функций:

• : округление определенного числа вверх;
• : возвращает модуль (абсолютное значение) указанного числа;
• : округление определенного числа вниз;
• : получение наибольшего общего делителя чисел и ;
• : возвращает сумму всех элементов итерируемого объекта;
• : возвращает (e^x)-1;
• : когда значение слишком мало, вычисление может привести к значительной потери в точности. может вернуть вывод с полной точностью.

В следующем примере показано использование перечисленных выше функций:

Python

import math

num = -4.28
a = 14
b = 8

num_list =
x = 1e-4 # Малое значение x

print(‘Число:’, num)
print(‘Округление числа вниз:’, math.floor(num))
print(‘Округление числа вверх:’, math.ceil(num))
print(‘Модуль числа:’, math.fabs(num))
print(‘Наибольший общий делитель a и b: ‘ + str(math.gcd(a, b)))
print(‘Сумма элементов списка: ‘ + str(math.fsum(num_list)))
print(‘e^x (при использовании функции exp()) равно:’, math.exp(x)-1)
print(‘e^x (при использовании функции expml()) равно:’, math.expm1(x))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

importmath num=-4.28 a=14 b=8 num_list=10,8.25,75,7.04,-86.23,-6.43,8.4 x=1e-4# Малое значение x print(‘Число:’,num) print(‘Округление числа вниз:’,math.floor(num)) print(‘Округление числа вверх:’,math.ceil(num)) print(‘Модуль числа:’,math.fabs(num)) print(‘Наибольший общий делитель a и b: ‘+str(math.gcd(a,b))) print(‘Сумма элементов списка: ‘+str(math.fsum(num_list))) print(‘e^x (при использовании функции exp()) равно:’,math.exp(x)-1) print(‘e^x (при использовании функции expml()) равно:’,math.expm1(x))

Вывод

Python

Число: -4.28
Округление числа вниз: -5
Округление числа вверх: -4
Модуль числа: 4.28
Наибольший общий делитель a и b: 2
Сумма элементов списка: 16.029999999999998
e^x (при использовании функции exp()) равно: 0.0001000050001667141
e^x (при использовании функции expml()) равно: 0.00010000500016667084

1 2 3 4 5 6 7 8

Число-4.28 Округлениечиславниз-5 Округлениечиславверх-4 Модульчисла4.28 Наибольшийобщийделительaиb2 Суммаэлементовсписка16.029999999999998 e^x(прииспользованиифункцииexp())равно0.0001000050001667141 e^x(прииспользованиифункцииexpml())равно0.00010000500016667084

К числу других математических функций относятся:

• : принимает два вещественных аргумента, возводит первый аргумент в степень, значением которой является второй аргумент, после чего возвращает результат. К примеру, эквивалентно выражению ;
• : возвращает квадратный корень определенного числа.

Примеры данных методов представлены ниже:

Возведение в степень

Python

math.pow(3, 4)

1	math.pow(3,4)

Вывод

Shell

81.0

1

81.0

Квадратный корень

Python

math.sqrt(81)

1	math.sqrt(81)

Вывод

Shell

9.0

1

9.0

Функция compare()

Функция сравнивает два числа с десятичной запятой и возвращает значения в зависимости от условий следующим образом:

• Возвращает -1, если первое десятичное число меньше второго десятичного числа.
• Возвращает 1, если первое десятичное число больше второго десятичного числа.
• Возвращает 0, если оба значения десятичной точки равны.

Пример:

import decimal as d

valx = d.Decimal(122.20)
valy = d.Decimal(123.01)

print("Value 1: ",valx)
print("Value 2: ",valy)

compare = valx.compare(valy)
print(compare)

Выход:

Value 1:  122.2000000000000028421709430404007434844970703125
Value 2:  123.0100000000000051159076974727213382720947265625
-1

Выбор случайного элемента из списка choice() модуль random

Метод используется для выбора случайного элемента из списка. Набор может быть представлен в виде списка или python строки. Метод возвращает один случайный элемент последовательности.

Пример использования в Python:

Python

import random

list =
print(«random.choice используется для выбора случайного элемента из списка — «, random.choice(list))

1 2 3 4 5

importrandom list=55,66,77,88,99 print(«random.choice используется для выбора случайного элемента из списка — «,random.choice(list))

Вывод:

Shell

random.choice используется для выбора случайного элемента из списка — 55

1	random.choiceиспользуетсядлявыбораслучайногоэлементаизсписка-55

Графические пользовательские интерфейсы в Python

Kivy

Kivy  —  это отличный фреймворк для создания приложений с возможностью запуска на всевозможных платформах. Любое создаваемое вами приложение Kivy будет работать на Linux, Mac, Windows, iOS и Android.

PyQt5

По моему мнению, PyQt5 является лучшим инструментом для создания GUI на Python. С ним вы получаете максимальный спектр возможностей и гибкость. В вашем распоряжении даже стиль CSS для оформления визуального облика приложения. Например, с помощью PyQt5 была создана Spider IDE. Если вы намерены создавать более сложные приложения для настольного компьютера, то лучшего варианта и не придумаешь.  

Tkinter

Tkinter  —  это библиотека “со стажем”, также применяемая для создания GUI. Она очень похожа на PyQt5 с точки зрения внешнего вида интерфейса, но обладает меньшими возможностями. На мой взгляд, ее легче освоить новичкам и тем, кто хочет получить быстрый результат без заморочек. 

Интерактивное программирование[править]

Особенно удобная возможность, предоставляемая Python — это возможность быстро проверить как работают инструкции или выражения в интерактивном режиме. Такие интерактивные оболочки называются shell. Мы уже пользовались ей как частью IDLE. Остановимся сейчас на ней поподробнее.

Interactive Shellправить

Программа, с которой мы работали в первом уроке, может быть напечатана строчка за строчкой с тем же конечным результатом:

>>> v0 = 5
>>> g = 9.81
>>> t = 0.6
>>> y = v0 * t - 0.5 * g * t ** 2
>>> print (y)
1.2342

Мы можем легко задать новое значение переменной, например для v0, и всегда способны проконтролировать, что новое значение присвоено, введя имя переменной напрямую или через инструкцию print::

>>> v0 = 6
>>> v0
6
>>> print (v0)
6

Следующий шаг — обновить выражения, в которых еще содержится старое значение, то есть нашу формулу для y. В таком редакторе как IPython можно найти предыдущее выражение, с помощью кнопок со стрелками. О возможностях этого редактора мы еще поговорим. А пока:

>>> y = v0 * t - 0.5 * g * t ** 2
>>> y
1.8341999999999996
>>> print (y)
1.8342

Причина, по которой мы получили сейчас два разных результата, в том, что, если вы просто пишите y, то вы увидите все знаки после точки, находящиеся в памяти компьютера (16), в то время как инструкция print ограничивает число знаков и, таким образом, дает ответ с достаточной точностью. Впрочем, в некоторых версиях Python автоматически округляет значение переменной.

Преобразование типаправить

Если вы ранее работали с другими языками программирования, то могли заметить, что мы пишем программы не заботясь о задании типов переменных (вернее даже типов объектов, на которые ссылаются переменные). Однако в этом уроке мы встретились с вопросом типов объектов, когда изучали ошибку целочисленного деления, которая научила нас более внимательно относиться к типам объектов. Следующий пример иллюстрирует функцию type( ) и то, как мы можем изменять тип объекта. Для начала, создадим объект типа int, на который будет ссылаться имя С:

>>> C = 21
>>> type(C)
<type 'int'>

Теперь мы преобразуем наш объект С типа int к соответствующему объекту типа float:

>>> C = float(C)     #  type  conversion
>>> type(C)
<type 'float'>
>>> C
21.0

В инструкции C = float(C) мы создали новый объект из оригинального объекта с тем же именем. Теперь имя С ссылается на новый объект. Изначальный объект типа int со значением 21 теперь недоступен, поскольку у него больше нет имени и автоматически удаляется из памяти.

Мы также можем сделать и обратное, то есть конвертировать объект типа float к объекту типа int:

>>> C = 20.9
>>> type(C)
<type 'float'>
>>> D = int(C) #  type  conversion
>>> type(D)
<type 'int'>
>>> D
20  # decimals  are  truncated  :-/

Как и следовало ожидать, переход к целым числам отрезал дробную часть. Если вас это не устраивает, и вам требуется округление до ближайшего целого, то существует простая функция:

>>> round(20.9)
21.0
>>> int(round(20.9))
21

Игра в кости с использованием модуля random в Python

Далее представлен код простой игры в кости, которая поможет понять принцип работы функций модуля random. В игре два участника и два кубика.

• Участники по очереди бросают кубики, предварительно встряхнув их;
• Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
• Участник, у которого в результате большее количество очков, выигрывает.

Код программы для игры в кости Python:

Python

import random

PlayerOne = «Анна»
PlayerTwo = «Алекс»

AnnaScore = 0
AlexScore = 0

# У каждого кубика шесть возможных значений
diceOne =
diceTwo =

def playDiceGame():
«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

for i in range(5):
#оба кубика встряхиваются 5 раз
random.shuffle(diceOne)
random.shuffle(diceTwo)
firstNumber = random.choice(diceOne) # использование метода choice для выбора случайного значения
SecondNumber = random.choice(diceTwo)
return firstNumber + SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза
for i in range(3):
# определим, кто будет бросать кости первым
AlexTossNumber = random.randint(1, 100) # генерация случайного числа от 1 до 100, включая 100
AnnaTossNumber = random.randrange(1, 101, 1) # генерация случайного числа от 1 до 100, не включая 101

if( AlexTossNumber > AnnaTossNumber):
print(«Алекс выиграл жеребьевку.»)
AlexScore = playDiceGame()
AnnaScore = playDiceGame()
else:
print(«Анна выиграла жеребьевку.»)
AnnaScore = playDiceGame()
AlexScore = playDiceGame()

if(AlexScore > AnnaScore):
print («Алекс выиграл игру в кости. Финальный счет Алекса:», AlexScore, «Финальный счет Анны:», AnnaScore, «\n»)
else:
print(«Анна выиграла игру в кости. Финальный счет Анны:», AnnaScore, «Финальный счет Алекса:», AlexScore, «\n»)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

importrandom PlayerOne=»Анна» PlayerTwo=»Алекс» AnnaScore= AlexScore=   # У каждого кубика шесть возможных значений diceOne=1,2,3,4,5,6 diceTwo=1,2,3,4,5,6 defplayDiceGame() «»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»» foriinrange(5) #оба кубика встряхиваются 5 раз random.shuffle(diceOne) random.shuffle(diceTwo) firstNumber=random.choice(diceOne)# использование метода choice для выбора случайного значения SecondNumber=random.choice(diceTwo) returnfirstNumber+SecondNumber print(«Игра в кости использует модуль random\n»)   #Давайте сыграем в кости три раза foriinrange(3) # определим, кто будет бросать кости первым AlexTossNumber=random.randint(1,100)# генерация случайного числа от 1 до 100, включая 100 AnnaTossNumber=random.randrange(1,101,1)# генерация случайного числа от 1 до 100, не включая 101 if(AlexTossNumber>AnnaTossNumber) print(«Алекс выиграл жеребьевку.») AlexScore=playDiceGame() AnnaScore=playDiceGame() else print(«Анна выиграла жеребьевку.») AnnaScore=playDiceGame() AlexScore=playDiceGame() if(AlexScore>AnnaScore) print(«Алекс выиграл игру в кости. Финальный счет Алекса:»,AlexScore,»Финальный счет Анны:»,AnnaScore,»\n») else print(«Анна выиграла игру в кости. Финальный счет Анны:»,AnnaScore,»Финальный счет Алекса:»,AlexScore,»\n»)

Вывод:

Shell

Игра в кости использует модуль random

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2

Алекс выиграл жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8

1 2 3 4 5 6 7 8 9 10

Игравкостииспользуетмодульrandom   Аннавыигралажеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны5ФинальныйсчетАлекса2   Аннавыигралажеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса2   Алексвыигралжеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса8

Вот и все. Оставить комментарии можете в секции ниже.

Комбинации элементов между собой

В библиотеке есть еще одна функция, связанная с перестановками и комбинациями, называемая . Эта функция является разновидностью функции , с той небольшой разницей, что она включает комбинации элементов между собой.

import itertools

values = 

com = itertools.combinations_with_replacement(values, 2)

for val in com:
	print(*val)

Выход:

1 1
1 2
1 3
1 4
2 2
2 3
2 4
3 3
3 4
4 4

Мы можем видеть четкое отличие вышеприведенного вывода от вывода с теми же параметрами при передаче в функцию .

Есть комбинации чисел, как будто их несколько экземпляров в списке. В основном это происходит потому, что, когда мы выбираем элемент из списка, вышеуказанная функция снова помещает то же значение, чтобы получить комбинации.

Еще пример. Наша задача — отобразить перестановку заданной строки. Здесь решаем эту проблему в python, используя перестановки встроенных функций (итерируемые).

Input : string = 'XYZ'
Output : XYZ
         XZY 
         YXZ
         YZX
         ZXY       
         ZYX

Алгоритм

Step 1: given string.
Step 2: Get all permutations of string.
Step 3: print all permutations.

Пример кода

from itertools import permutations 
def allPermutations(str1): 
   # Get all permutations of string 'ABC' 
   per = permutations(str1) 
   # print all permutations
   print("Permutation Of this String ::>")
   for i in list(per): 
      print (''.join(i)) 
# Driver program 
if __name__ == "__main__": 
   str1 = input("Enter the string ::>")
   allPermutations(str1) 

Вывод

Enter the string ::> abc
Permutation Of this String ::>
abc
acb
bac
bca
cab
cba

Функция exp() — вычисление экспоненты

Функция вычисляет значение экспоненты, то есть e ^ x конкретного числа переданной десятичной точки.

Синтаксис:

decimal.Decimal(decimal-number).exp()

Пример:

import decimal as d

d.getcontext().prec = 5

#Intializing with an addition operation
val = d.Decimal(12.201) + d.Decimal(12.20)

#Calculating exponential of the decimal value
exp = val.exp()

#variable with no calculations
no_math = d.Decimal(1.131231)

print("Sum: ",val)
print("Exponential: ", exp)
print(no_math)

Выход:

Decimal Number:  24.401                                                                                                       
3.9557E+10                                                                                                                    
1.131231000000000097571728474576957523822784423828125   

Следует помнить, что значение точности применяется, когда вы выполняете математические операции с двумя десятичными знаками, а не когда вы напрямую инициируете переменную со значениями, как показано с переменной «no_math» выше.

Арифметические операции на сложных числах

Подобно реальным числам, комплексные числа также могут быть добавлены, вычтены, умножены и разделены. Давайте посмотрим на то, как мы могли бы сделать это в Python.

a = 1 + 2j
b = 2 + 4j
print('Addition =', a + b)
print('Subtraction =', a - b)
print('Multiplication =', a * b)
print('Division =', a / b)

Выход :

Addition = (3+6j)
Subtraction = (-1-2j)
Multiplication = (-6+8j)
Division = (2+0j)

Примечание : В отличие от реальных чисел, мы не можем сравнить два комплексных номера. Мы можем сравнивать только свои реальные и мнимые части индивидуально, поскольку они являются реальными числами. Ниже фрагмент доказывает это.

>>> a
(4+3j)
>>> b
(4+6j)
>>> a < b
Traceback (most recent call last):
  File "", line 1, in 
TypeError: '<' not supported between instances of 'complex' and 'complex'

Фаза комплексного числа

Фаза комплексного числа – это угол между действительной осью и вектором, представляющим мнимую часть. Изображение ниже иллюстрирует фазу комплексного числа и то, как получить это значение с помощью модулей cmath и math.

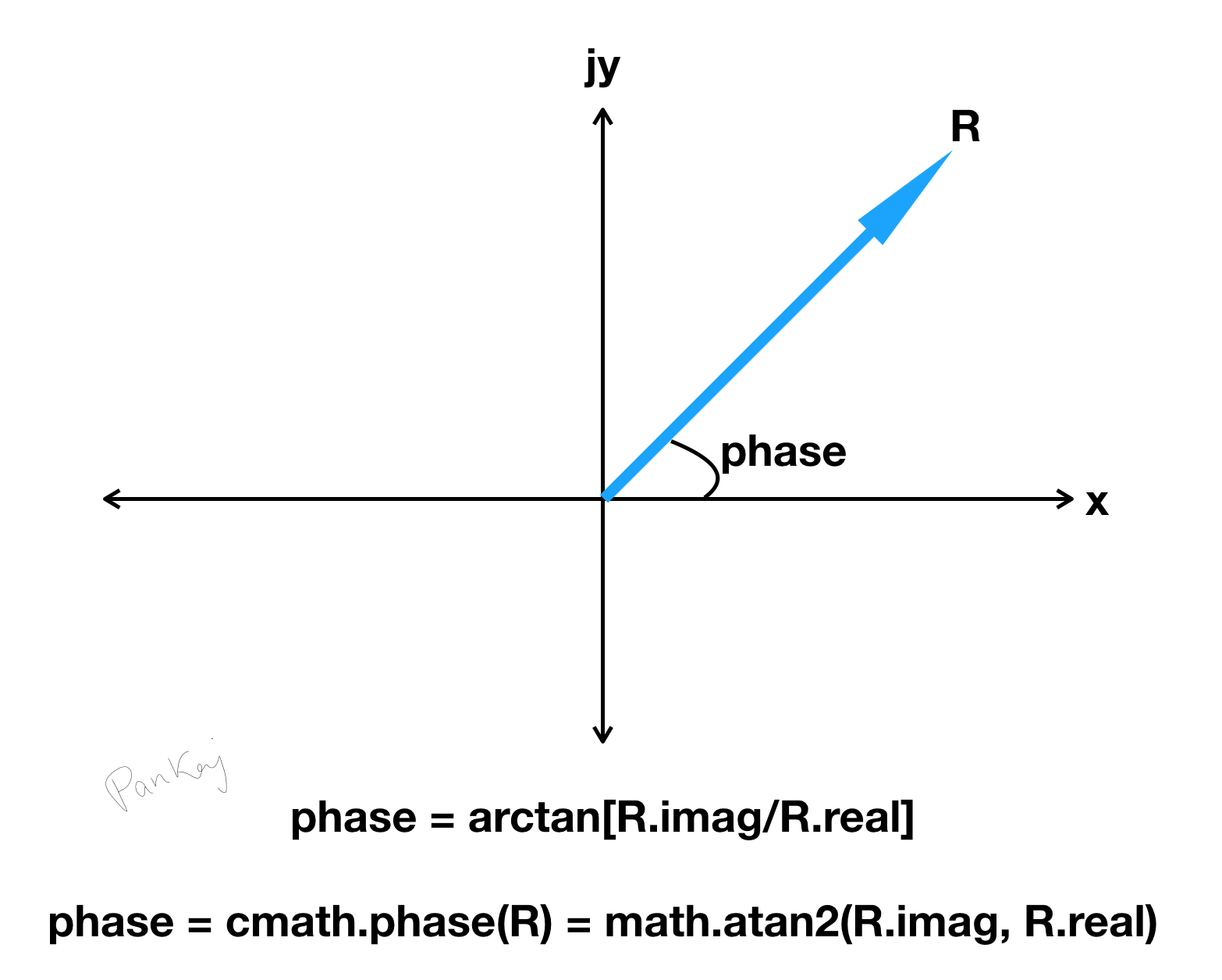
Обратите внимание, что фаза, возвращаемая модулями math и cmath, выражается в радианах, мы можем использовать функцию numpy.degrees(), чтобы преобразовать ее в градусы. Диапазон фазы – от -π до + π (от -pi до + pi) в радианах, что эквивалентно от -180 до +180 градусов

import cmath, math, numpy

c = 2 + 2j

# phase
phase = cmath.phase(c)
print('2 + 2j Phase =', phase)
print('Phase in Degrees =', numpy.degrees(phase))
print('-2 - 2j Phase =', cmath.phase(-2 - 2j), 'radians. Degrees =', numpy.degrees(cmath.phase(-2 - 2j)))

# we can get phase using math.atan2() function too
print('Complex number phase using math.atan2() =', math.atan2(2, 1))

Вывод:

2 + 2j Phase = 0.7853981633974483
Phase in Degrees = 45.0
-2 - 2j Phase = -2.356194490192345 radians. Degrees = -135.0
Complex number phase using math.atan2() = 1.1071487177940904

Гиперболические функции

math.sinh(x)

Возвращает гиперболический синус угла x заданного в радианах.

math.cosh(x)

Возвращает гиперболический косинус угла x заданного в радианах.

math.tanh(x)

Возвращает гиперболический тангенс угла x заданного в радианах.

math.asinh(x)

Возвращает гиперболический арксинус значения x, т.е. возвращает такое значение угла y (заданного в радианах) при котором .

math.acosh(x)

Возвращает гиперболический арккосинус значения x, т.е. возвращает такое значение угла y (заданного в радианах) при котором .

math.atanh(x)

Возвращает гиперболический арктангенс значения x, т.е. возвращает такое значение угла y (заданного в радианах) при котором .