Что такое корреляция
Содержание:
- Как вы можете рассчитать корреляцию с помощью Excel? — 2019
- Распространенные заблуждения
- Вычисление коэффициента посредством мастера функций
- Примеры решений онлайн: линейная регрессия
- 9.1.3. Простая линейная регрессия
- Как выполняется корреляция в Excel?
- Значения коэффициента корреляции
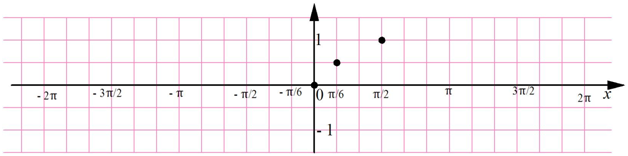
- Визуализация корреляции
Как вы можете рассчитать корреляцию с помощью Excel? — 2019
a:
Корреляция измеряет линейную зависимость двух переменных. Измеряя и связывая дисперсию каждой переменной, корреляция дает представление о силе взаимосвязи. Или, говоря иначе, корреляция отвечает на вопрос: сколько переменная A (независимая переменная) объясняет переменную B (зависимую переменную)?
Формула корреляции
Корреляция объединяет несколько важных и связанных статистических понятий, а именно дисперсию и стандартное отклонение. Разница — дисперсия переменной вокруг среднего, а стандартное отклонение — квадратный корень дисперсии.
Формула:
Поскольку корреляция требует оценки линейной зависимости двух переменных, то, что действительно необходимо, — это выяснить, какая сумма ковариации этих двух переменных и в какой степени такая ковариация отраженные стандартными отклонениями каждой переменной в отдельности.
Общие ошибки с корреляцией
Самая распространенная ошибка — предполагать, что корреляция, приближающаяся +/- 1, статистически значима. Считывание, приближающееся +/- 1, безусловно увеличивает шансы на фактическую статистическую значимость, но без дальнейшего тестирования это невозможно узнать.
Статистическое тестирование корреляции может усложняться по ряду причин; это совсем не так просто. Критическое предположение о корреляции состоит в том, что переменные независимы и связь между ними является линейной.
Вторая наиболее распространенная ошибка — забыть нормализовать данные в единую единицу. Если вычислять корреляцию по двум бетам, то единицы уже нормализованы: сама бета является единицей
Однако, если вы хотите скорректировать акции, важно, чтобы вы нормализовали их в процентном отношении, а не изменяли цены. Это происходит слишком часто, даже среди профессионалов в области инвестиций
Для корреляции цен на акции вы, по сути, задаете два вопроса: каково возвращение за определенное количество периодов и как этот доход коррелирует с возвратом другой безопасности за тот же период? Это также связано с тем, что корреляция цен на акции затруднена: две ценные бумаги могут иметь высокую корреляцию, если доход составляет ежедневно процентов за последние 52 недели, но низкая корреляция, если доход ежемесячно > изменения за последние 52 недели. Какая из них лучше»? На самом деле нет идеального ответа, и это зависит от цели теста. ( Улучшите свои навыки excel, пройдя курс обучения Excel в Академии Excel. ) Поиск корреляции в Excel
Существует несколько методов расчета корреляции в Excel
Самый простой способ — получить два набора данных и использовать встроенную формулу корреляции:
Это удобный способ расчета корреляции между двумя наборами данных. Но что, если вы хотите создать корреляционную матрицу во множестве наборов данных? Для этого вам нужно использовать плагин анализа данных Excel. Плагин можно найти на вкладке «Данные» в разделе «Анализ».
Выберите таблицу возвратов. В этом случае наши столбцы имеют названия, поэтому мы хотим установить флажок «Ярлыки в первой строке», поэтому Excel знает, как обрабатывать их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.
Как только вы нажмете enter, данные будут автоматически сделаны. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Распространенные заблуждения
Корреляция и причинно-следственная связь
Традиционное изречение, что « корреляция не подразумевает причинно-следственную связь », означает, что корреляция не может использоваться сама по себе для вывода причинной связи между переменными. Это изречение не должно означать, что корреляции не могут указывать на потенциальное существование причинно-следственных связей. Однако причины, лежащие в основе корреляции, если таковые имеются, могут быть косвенными и неизвестными, а высокие корреляции также пересекаются с отношениями идентичности ( тавтологиями ), где не существует причинного процесса. Следовательно, корреляция между двумя переменными не является достаточным условием для установления причинно-следственной связи (в любом направлении).
Корреляция между возрастом и ростом у детей довольно прозрачна с точки зрения причинно-следственной связи, но корреляция между настроением и здоровьем людей менее очевидна. Приводит ли улучшение настроения к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или в основе обоих лежит какой-то другой фактор? Другими словами, корреляция может рассматриваться как свидетельство возможной причинной связи, но не может указывать на то, какой может быть причинная связь, если таковая имеется.
Простые линейные корреляции
Четыре набора данных с одинаковой корреляцией 0,816
Коэффициент корреляции Пирсона указывает на силу линейной связи между двумя переменными, но его значение, как правило, не полностью характеризует их взаимосвязь. В частности, если условное среднее из дано , обозначается , не является линейным в , коэффициент корреляции будет не в полной мере определить форму .
Y {\ displaystyle Y} Икс {\ displaystyle X} E ( Y ∣ Икс ) {\ displaystyle \ operatorname {E} (Y \ mid X)} Икс {\ displaystyle X} E ( Y ∣ Икс ) {\ displaystyle \ operatorname {E} (Y \ mid X)}
Прилегающие изображение показывает разброс участков из квартет энскомбы , набор из четырех различных пар переменных , созданный Фрэнсис Анскомбами . Четыре переменные имеют одинаковое среднее значение (7,5), дисперсию (4,12), корреляцию (0,816) и линию регрессии ( y = 3 + 0,5 x ). Однако, как видно на графиках, распределение переменных сильно отличается. Первый (вверху слева), кажется, распределен нормально и соответствует тому, что можно было бы ожидать, рассматривая две коррелированные переменные и следуя предположению о нормальности. Второй (вверху справа) не распространяется нормально; Хотя можно наблюдать очевидную взаимосвязь между двумя переменными, она не является линейной. В этом случае коэффициент корреляции Пирсона не указывает на то, что существует точная функциональная взаимосвязь: только степень, в которой эта взаимосвязь может быть аппроксимирована линейной зависимостью. В третьем случае (внизу слева) линейная зависимость идеальна, за исключением одного выброса, который оказывает достаточное влияние, чтобы снизить коэффициент корреляции с 1 до 0,816. Наконец, четвертый пример (внизу справа) показывает другой пример, когда одного выброса достаточно для получения высокого коэффициента корреляции, даже если связь между двумя переменными не является линейной.
y {\ displaystyle y}
Эти примеры показывают, что коэффициент корреляции как сводная статистика не может заменить визуальный анализ данных. Иногда говорят, что примеры демонстрируют, что корреляция Пирсона предполагает, что данные следуют нормальному распределению , но это неверно.
Вычисление коэффициента посредством мастера функций
Предположим, что требуется установить связь между затратами на рекламу и объемом продаж какой-либо продукции. Для этого будем использовать коэффициент корреляции в Excel.
Порядок действий:
- Кликнуть по ячейке, в которой должен появиться результат.
- Нажать кнопку «Вставить формулу».
- В появившемся окне выбрать категорию «Полный алфавитный перечень».
- Найти и активировать функцию «КОРРЕЛ».
- Кликнуть «ОК».
- В открывшемся окне аргументов поставить курсор в поле «Массив 1», выделить первый столбец с данными.
- Поставить курсор в поле «Массив 2», выделить второй столбец из таблицы.
- Кликнуть «ОК».
В выделенной ячейке появляется результат вычислений корреляции в Excel.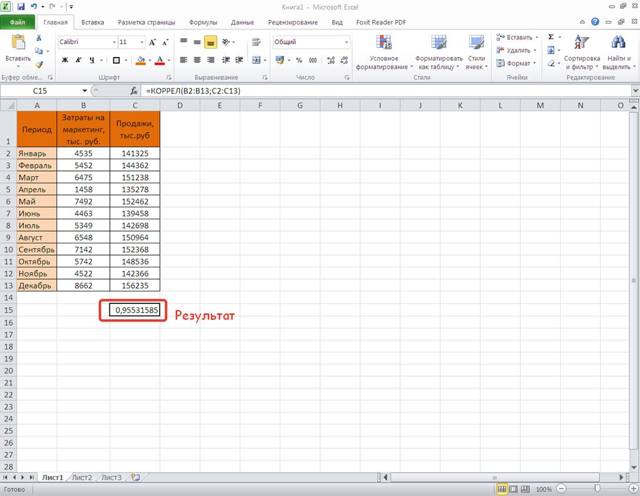
Расчёт с помощью пакета анализа
Прежде чем воспользоваться инструментом корреляционного анализа, его нужно активировать. Для этого необходимо выполнить следующие действия:
- Выполнить действия «Файл» — «Сведения» — «Параметры».
- В появившемся окне перейти в раздел «Надстройки». В нижней части окна в выпадающем списке выбрать «Надстройки Excel». Нажать кнопку «Перейти».
- В открывшемся окне «Надстройки» следует отметить пункт «Пакет анализа» и нажать «ОК»
Чтобы воспользоваться пакетом, следует:
- На панели задач активировать вкладку «Данные».
- Нажать кнопку «Анализ данных».
- В новом окне выделить строку «Корреляция» и нажать «ОК». Появится окно с параметрами.
- Для выбора входного интервала необходимо установить курсор в соответствующее поле и выделить сразу оба столбца.
- Параметр группировки следует отметить «по столбцам». Вывод результатов возможен в указанное место, на новый лист или в новую книгу.
- Следует отметить соответствующее поле.
Работа со сводными таблицами в MS Excel
После указание всех параметров следует нажать «ОК».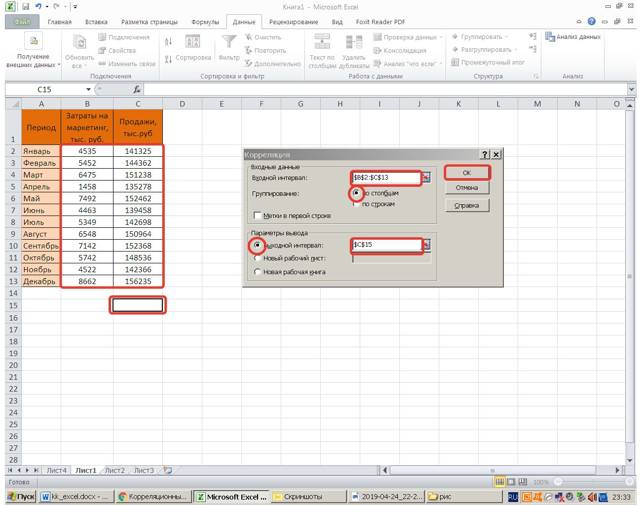
Значение получилось тем же, что и в первом случае.
Поле корреляции (диаграмма рассеяния)
Корреляционное поле — это графическое отображение исходных данных. По расположению точек можно определить наличие зависимости и ее характер.
В редакторе Excel построение выполняется с помощью инструмента «Диаграмма»:
- Выделить столбцы с данными.
- Кликнуть «Вставка» — «Точечная» — «Точечная с маркерами».
- Результат построения корреляционной матрицы.
- По расположению точек на диаграмме можно сделать вывод о том, что прослеживается сильная положительная корреляционная зависимость между величиной затрат на маркетинг и объемом продаж.
- Для того, чтобы использовать диаграмму в практических целях, можно добавить линию тренда и уравнение. Для этого нужно выполнить следующие действия:
- Кликнуть правой кнопкой мыши на любой точке диаграммы.
- В контекстном меню выбрать «добавить линию тренда».
- Настроить параметры линии тренда (можно оставить по умолчанию).
- Нажать кнопку «закрыть».
Примеры использование корреляционного анализа
Как уже отмечалось выше, вычислить соотношение можно между любыми числовыми величинами. Обнаруженная высокая корреляция позволяет прогнозировать протекание каких-либо процессов в научных исследованиях, бизнесе, общественной жизни.
В рассмотренном выше примере была установлена высокая положительная корреляция между затратами на рекламу и объемом продаж определенного вида продукции. Кроме того, была определена формула, связывающая эти два показателя. Это исследование позволяет руководителю предприятия грамотно спланировать затраты на рекламу, с учетом необходимого размера продаж.
Другие примеры использования коэффициента корреляции:
Что делать, если лист или книга в Excel защищены паролем – как снять защиту
Редактор электронных таблиц Microsoft Excel является удобным инструментом для вычисления и наглядного представления результатов вычисления коэффициента корреляции.
Примеры решений онлайн: линейная регрессия
Простая выборка
Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.
Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.
Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.
Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью. Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.
Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
Корреляционная таблица
Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице
Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.
Решение об исследовании зависимости (4 страницы)
Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.
Коэффициент корреляции
Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?
Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $\overline{X}=82$ у.е., $S_x=31$ у.е., $\overline{Y}=39$ у.е., $S_y=29$ у.е., $\overline{XY} =3709$ (у.е.)2. При $\alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.
Нужно решить задачи по на тему регрессия и корреляция?
Оставьте заявку сегодня
9.1.3. Простая линейная регрессия
Применение линейного регрессионного анализа имеет специфические черты по сравнению с другими методами обработки данных. Его непосредственное употребление ограничено, в основном, задачами о предсказании значений зависимой переменной по известным значениям аргумента (или аргументов), что в психологии задача не слишком востребованная. Однако, во-первых, линейная регрессия входит как часть во многие другие методы (например, анализ медиации и модерации, о которых речь пойдет в следующей главе), и, во-вторых, служит простым примером отыскания наилучших параметров для модели определенного типа, и психологу полезно понимать суть этого метода. Качество каждого набора параметров, а затем и модели в целом, оценивается процентом дисперсии, который остался вне предсказаний, сделанных моделью по данным значениям аргументов. Замечательным результатом для читателя будет здесь улавливание аналогий с двухфакторным дисперсионным анализом.
Как выполняется корреляция в Excel?
«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.
Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).
Использование корреляции
Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.
Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.
Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.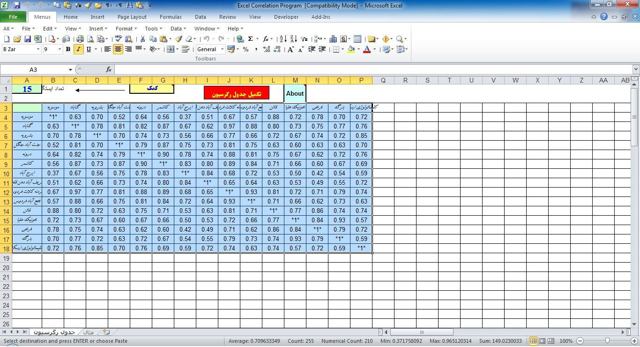
Как выполнить корреляцию в Excel?
Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:
- Выбрать пустую ячейку, в которую будет выведен результат расчетов.
- Нажать в главном меню Excel пункт «Формулы».
- Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
- В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
- В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
- Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.
Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).
Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.
Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.
Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.
Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.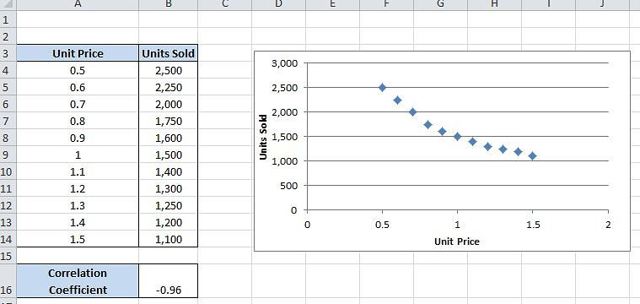
Значения коэффициента корреляции
Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.
- 0-0,3 – корреляционная связь очень слабая;
- 0,3-0,5 – слабая;
- 0,5-0,7 – средней силы;
- 0,7-0,9 – высокая;
- 0,9-1 – очень высокая сила корреляции.
Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.
Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:
- очень сильная – показатели ±0,7 — ±1;
- средняя – показатели ±0,3 — ±0,699;
- очень слабая – показатели 0 — ±0,299.
Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.
История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
- Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
- Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
- Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
- Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов
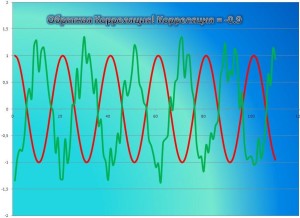
Визуализация корреляции
Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:
Этот пример сгенерирует следующий ниже график:
Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:
Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.