Как найти в python остаток от деления?

Базовые структуры данных Python

К ним относятся:

Целые числа

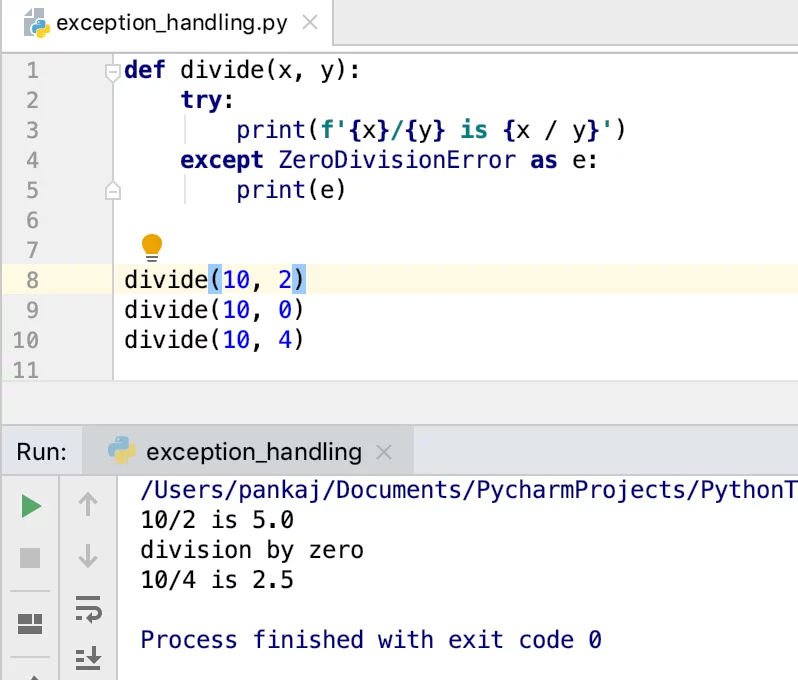
Над ними можно производить операции сложения (a + b), вычитания (a — b), деления (a / b) – в этом случае результат может стать вещественным если не делится нацело, умножения (a * b). Есть операция остаток от деления (a % b), например, если разделить 5 на 2 (5 % 2 = 1), то остаток от деления будет 1.

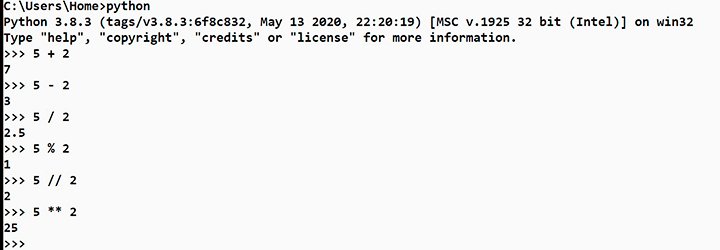
Остаток от деления записывается при помощи знака процент %. При помощи двойного слэша ( // ) можно выполнить деление нацело, при этом отбрасывается дробная часть. Например, если разделить нацело 5 на 2, то мы получим 2 (5 // 2 = 2), остаток 1 не будет учитываться.

Числа можно сравнивать. Для этого используются сравнения больше ( > ), меньше ( < ), больше или равно ( >= ), меньше или равно ( <= ), равенства ( == ) – записывается как двойное равенство, не равно ( != ) – записывается как восклицательный знак и равно. Результатом выполнения этих операций является истина или ложь (True) или (False).

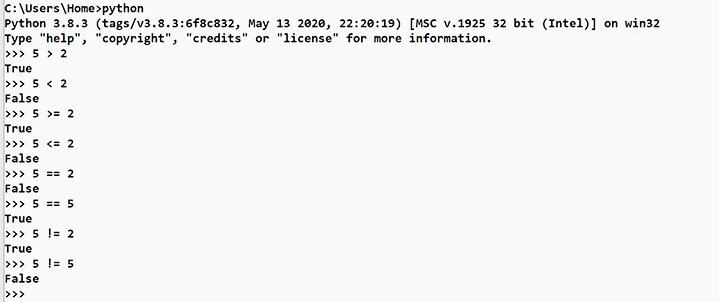
Также можно делать тройное сравнение, например, (2 < 4 < 6)  будет «True» — истина, (5 < 2 < 7) даст результат ложь «False». При помощи тройного сравнения можно проверить попадает ли в нужный диапазон

Вещественные типы данных

Это числа с дробной частью или еще они называются с плавающей точкой. Над ним можно производить все действия применимые к целым. Но операции над вещественными числами происходят с округлением, что может привести к ошибкам. Если сложить (0,3 + 0,3 + 0,3 +0,1), то получим 0.9999999999999999.

Для более точных вычислений в языке Python существуют числа с заданной точностью. Все операции между числами с плавающей точкой дают вещественные величины, между вещественным и целым также являются вещественными.

Можно возводить в дробную степень, что фактически является извлечением корня. Вещественное число можно конвертировать в целое ( int(41.3) = 41), а целое можно привести к вещественному ( float(41) = 41.0 ).

Для числовых данных приоритетным является выражение, заключенное в скобки. Далее по приоритетам идет возведение в степень, затем умножение и деление, сложение и вычитание, унарный минус.

Булевы значения

К ним применимы операции булевой алгебры. К ним относятся:

—  Логическое сложение – дизъюнкция («или» — на английском языке «or»). В этом случае если есть хотя бы одно «True», то выражение будет истинно

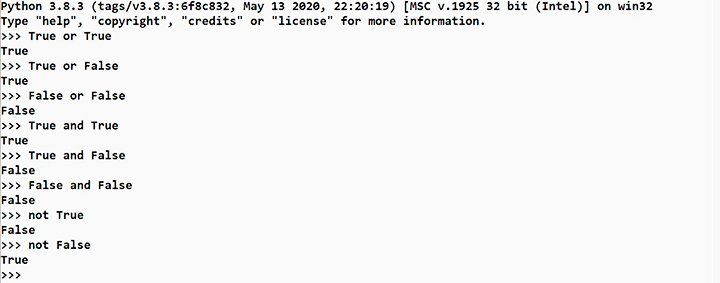
— Логическое умножение – конъюнкция («и» — «and»). Выражение истинно, когда все его элементы одинаковы.

— Логическое отрицание – инверсия («не» — «not»). Отрицание меняет истину на ложь, а ложь на истину.

Выполнение операции деления

При делении результирующий вектор является значениями частного после выполнения операции деления над двумя векторами.

Для лучшего понимания рассмотрим приведенный ниже пример.

x = и y = – два вектора. Таким образом, результирующий вектор v будет таким:

v = x / y v = x / y .

Давайте теперь реализуем вышеуказанную концепцию.

Пример:

import numpy as np 
 
lst1 =  
lst2 = 
 
vctr1 = np.array(lst1) 
 
vctr2= np.array(lst2) 
 
print("Vector created from a list 1:") 
print(vctr1) 
print("Vector created from a list 2:") 
print(vctr2) 
 
vctr_div = vctr1/vctr2
print("Division of two vectors: ",vctr_div)

Вывод:

Vector created from a list 1:

Vector created from a list 2:

Multiplication of two vectors:  

Что такое структура данных в языке программирования Python

Структуры данных в Python служат для написания программ, которые могут быть как простыми, так и достаточно сложными. Они бывают линейные, нелинейные и специфические.

К линейным структурам данных Python можно отнести массивы, матрицы, стек, очередь, связанный список. К нелинейным график, двоичное дерево, кучу, хэш-таблицу. Специфическими являются кортежи, словари, списки.

Также структуры данных в Питоне классифицируются как базовые, встроенные, динамические, упорядоченные, простейшие, собственные, общие, связанные.

Основные типы данных в Python это числа целые, с плавающей точкой, комплексные, строки, булев тип, тип none, исключения, байты, файлы, множества, функции, кортежи, словари, списки, строки.

Программа на Python с векторизацией и построением графиков

Вернемся к задаче, описывающей вертикальное положение \( y \) мяча после
подбрасывания. Предположим, что нас интересуют значения \( y \) в
каждую миллисекунду первой секунды полета. Это требует повторения
вычисления \( y = v_0 t — 0.5 g t^2 \) тысячу раз.

Также построим график зависимости \( y \) от \( t \) на отрезке
\( \). Построение такого графика на компьютере подразумевает
рисование прямых отрезков между точками кривой, поэтому нам
понадобится много точек, чтобы создать визуальный эффект гладкой
кривой. Тысячи точек, которые мы вычислим, нам будет достаточно для
этого.

Реализацию таких вычислений и построения графика может быть
реализовано следующим сценарием (ball_plot.py):

# -*- coding: utf-8 -*-

from numpy import linspace
import matplotlib.pyplot as plt

v0 = 5
g = 9.81
t = linspace(, 1, 1001)

y = v0*t - 0.5*g*t**2

plt.plot(t, y)
plt.xlabel(u't (с)')
plt.ylabel(u'y (м)')
plt.show()

def height(t):
	h =  v0*t - 0.5*g*t**2
	return h

h = lambda t: v0*t - 0.5*g*t**2

Замечание

В нашем сценарии для символьных аргументов мы использовали префикс
(например, ), чтобы указать, что
символы содержатся в кодировке UTF8.

Данный сценарий строит график зависимости вертикального положения мяча
от времени (см. рис. :numref:`%s`). Отметим, что строки для
вычисления из сценария ball.py из раздела
мало изменены, но значение
вычисляется для тысячи точек.

Рассмотрим различия рассматриваемого сценария от предыдущих. Первое
отличие это строки, которые могли выглядеть следующим образом:

from numpy import *
from matplotlib.pyplot import *

Мы видим, что является модулем Python. Этот модуль содержит
огромный функционал для математических вычислений, а модуль
реализует возможности для построения двумерных
графиков. Приведенные выше строки представляют быстрый способ загрузки
всего функционала, связанного с вычислениями и построением
графиков. Однако, фактически мы используем только несколько функций в
нашем сценарии: , , и
. Многие разработчики считают, что мы должны импортировать
только то, что нам нужно, а не весь возможный функционал:

from numpy import linspace
from matplotlib.pyplot import plot, xlabel, ylabel

Другие предлагают способ импорта, когда используется префикс для
функций модуля

import numpy as np
import matplotlib.pyplot as plt

...

t = np.linspace(, 1, 1001)
   
...

plt.plot(x,y)

Мы будем использовать все три способа. В нашем сценарии мы
использовали два из них.

from numpy import linspace
import matplotlib.pyplot as plt

Рисунок 1: График, построенный с помощью нашего сценария.

Функция принимает три аргумента и, в общем случае,
вызывается следующим образом:

linspace(start, stop, n)

Функция генерирует равноотстоящих координат,
начинающихся со значения , и заканчивающихся
. Выражение создает 1001 координату
от 0 до 1 включительно. Математически это означает, что отрезок
\( \) разбивается на 1000 равных отрезков и значения координат
в этом случае вычисляются следующим образом: \( t_i = i/1000,\ i = 0, 1,
\ldots, 1000 \).

Функция возвращает объект класса ,
т.е. некоторый набор чисел (массив). При выполнении арифметических операций с
такими объектами, на самом деле эти операции осуществляются для каждого
элемента массива. В результате получается аналогичный массив из 1001
элемента, который сохраняется в переменную . Таким образом
также является массивом.

Такой подход вычисления нескольких чисел в одну строку называется
векторизацией. Этот способ очень удобен, так как сокращает не только
количество кода, но и время вычислений по сравнению с использованием
циклов или .

Команды для построения графиков достаточно просты:

1. означает построение графика зависимости от

2. помещает текст на оси .

3. помещает текст на оси .

Кубический корень

Само название функции намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:

Вышеуказанное соотношение несложно доказать и для других степеней вида .

В случае с квадратным или кубическим корнем эти операции действительно эквивалентны, но, вообще говоря, в математике извлечение корня и возведение в дробную степень имеют существенные отличия при рациональных степенях вида m/n, где m != 1. Формально, в дробно-рациональную степень можно возводить только положительные вещественные числа. В противном случае возникают проблемы:

Таким образом, извлечь кубический корень в Python можно следующим образом:

Или же:

Как и где изучать Python самостоятельно

Изучать типы и структуры данных в Python лучше постепенно, переходя от простых структур данных и работы с ними к более сложным конструкциям и алгоритмам. Можно найти достаточно много бесплатных курсов в интернете, например, на ресурсе Stepik и многих других.

Есть много книг и самоучителей по программированию на языке Python, где подробно разбираются структуры данных, типы данных с примерами и задачами для самостоятельного выполнения.

Также на платформе ютуб находится множество видеороликов и обучающих материалов по данной теме. Например, МФТИ выкладывает лекции по программированию на Python в свободном доступе на YouTube.

Логические операции с десятичным модулем

Decimal содержит набор встроенных функций для выполнения логических операций с десятичными числами, таких как AND, OR, XOR и т. Д.

• Функция logical_and(): выполняет операцию логического И над двумя десятичными числами и возвращает результат.
• Функция logical_or(): выполняет операцию логического ИЛИ над двумя десятичными числами и возвращает результат.
• Функция logical_xor(): выполняет логическую операцию XOR над двумя десятичными числами и возвращает результат.

#Syntax for logical_and() function-
decimal1.logical_and(decimal2)

#Syntax for logical_or() function-
decimal1.logical_or(decimal2)

#Syntax for logical_xor() function-
decimal1.logical_xor(decimal2)

Пример:

import decimal as d

valx = d.Decimal(1001)
valy = d.Decimal(1111)

print("Value 1: ",valx)
print("Value 2: ",valy)

AND = valx.logical_and(valy)
print("The logical AND value of the two decimals: ",AND)

OR = valx.logical_or(valy)
print("The logical OR value of the two decimals: ",OR)

XOR = valx.logical_xor(valy)
print("The logical XOR value of the two decimals: ",XOR)

Выход:

Value 1:  1001
Value 2:  1111
The logical AND value of the two decimals:  1001
The logical OR value of the two decimals:  1111
The logical XOR value of the two decimals:  110

Числа: целые, вещественные, комплексные

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y)	x y по модулю (если модуль задан)

Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).

Битовые операции

Над целыми числами также можно производить битовые операции

x | y	Побитовое или
x ^ y	Побитовое исключающее или
x & y	Побитовое и
x > y	Битовый сдвиг вправо

x

Инверсия битов

Дополнительные методы

int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

Системы счисления

Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:

• int(, ) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
• bin(x) — преобразование целого числа в двоичную строку.
• hex(х) — преобразование целого числа в шестнадцатеричную строку.
• oct(х) — преобразование целого числа в восьмеричную строку.

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

Простенькие примеры работы с числами:

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.

Модуль math предоставляет более сложные математические функции.

Модуль random реализует генератор случайных чисел и функции случайного выбора.

Также для работы с комплексными числами используется также модуль cmath.

Дополнительные методы и операции в Python

В эти операции входят:
• int.bit_length() — количество бит, которое необходимо, чтобы представить число в двоичном виде без учёта лидирующих нулей и знака;
• int.to_bytes(length, byteorder, *, signed=False) — метод возвращает строку байтов, которые представляют это число;
• classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращение числа из заданной строки байтов.

Пример работы последнего метода:

>>>
>>> int.from_bytes(b'\x00\x10', byteorder='big')
16
>>> int.from_bytes(b'\x00\x10', byteorder='little')
4096
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True)
-1024
>>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False)
64512
>>> int.from_bytes(, byteorder='big')
16711680

Быстрый алгоритм Евклида

Но у этого
алгоритма есть один существенный недостаток: если мы введем два вот таких
числа:

100000000 и 2

то этот алгоритм
начнет довольно долго работать и понятно почему, здесь мы получим большое
количество вычитаний 2. Эти вычитания будут происходить до тех пор, пока двойка
укладывается в оставшееся число. И мы здесь без всяких вычитаний сразу можем
сказать, что на последнем шаге будет вот такая операция:

4-2 = 2

После чего оба
числа станут равными и НОД будет равен двум. Так вот, чтобы без лишних операций
сразу определить на сколько будут отличаться два числа после серии вычитаний,
достаточно взять целый остаток от деления. Например:

100000000 % 2 =
0

Это значит, что
большее число можно полностью составить из суммы двоек. Следовательно, они оба
делятся на два нацело и их НОД равен 2. Хорошо, а если вместо 2 взять 3. В этом
случае имеем:

100000000 % 3 =
1

и далее уже
можно рассматривать два числа: 3 и 1. Причем, для них также можно выполнить
такую же операцию:

3 % 1 = 1
1 % 1 = 0

Все, получили
НОД, равный 1. И смотрите, здесь на каждой итерации большее число делится на
меньшее. Поэтому быстрый алгоритм Евклида можно записать так:

пока меньшее число больше 0
        большему числу присваиваем остаток от деления на меньшее число
выводим большее число

Реализуем этот алгоритм. И договоримся, что большее число будем хранить в a, меньшее – в b.

a = int(input("Введите 1-е натуральное число: "))
b = int(input("Введите 2-е натуральное число: "))
sa = a; sb = b
b = min(sa, sb)
a = max(sa, sb)
while b:
    a,b = b, a%b
 
print("НОД(%d, %d) = %d"%(sa,sb,a))

В этом алгоритме
используется свойство:

a%b = c,  c < b

то есть, остаток
всегда будет меньше числа b. Значит, из двух чисел c и b большим будет b, а меньшим – c. Именно поэтому
в программе записано такое множественное присваивание:

a,b = b, a%b

Мы здесь переменной a
присваиваем
значение b, а b
становится
равным остатку от деления. Это гарантируется, что a
>=
b.

Видео по теме

Python 3 #1: установка и запуск интерпретатора языка

Python 3 #2: переменные, оператор присваивания, типы данных

Python 3 #3: функции input и print ввода/вывода

Python 3 #4: арифметические операторы: сложение, вычитание, умножение, деление, степень

Python 3 #5: условный оператор if, составные условия с and, or, not

Python 3 #6: операторы циклов while и for, операторы break и continue

Python 3 #7: строки — сравнения, срезы строк, базовые функции str, len, ord, in

Python 3 #8: методы строк — upper, split, join, find, strip, isalpha, isdigit и другие

Python 3 #9: списки list и функции len, min, max, sum, sorted

Python 3 #10: списки — срезы и методы: append, insert, pop, sort, index, count, reverse, clear

Python 3 #11: списки — инструмент list comprehensions, сортировка методом выбора

Python 3 #12: словарь, методы словарей: len, clear, get, setdefault, pop

Python 3 #13: кортежи (tuple) и операции с ними: len, del, count, index

Python 3 #14: функции (def) — объявление и вызов

Python 3 #15: делаем «Сапер», проектирование программ «сверху-вниз»

Python 3 #16: рекурсивные и лямбда-функции, функции с произвольным числом аргументов

Python 3 #17: алгоритм Евклида, принцип тестирования программ

Python 3 #18: области видимости переменных — global, nonlocal

Python 3 #19: множества (set) и операции над ними: вычитание, пересечение, объединение, сравнение

Python 3 #20: итераторы, выражения-генераторы, функции-генераторы, оператор yield

Python 3 #21: функции map, filter, zip

Python 3 #22: сортировка sort() и sorted(), сортировка по ключам

Python 3 #23: обработка исключений: try, except, finally, else

Python 3 #24: файлы — чтение и запись: open, read, write, seek, readline, dump, load, pickle

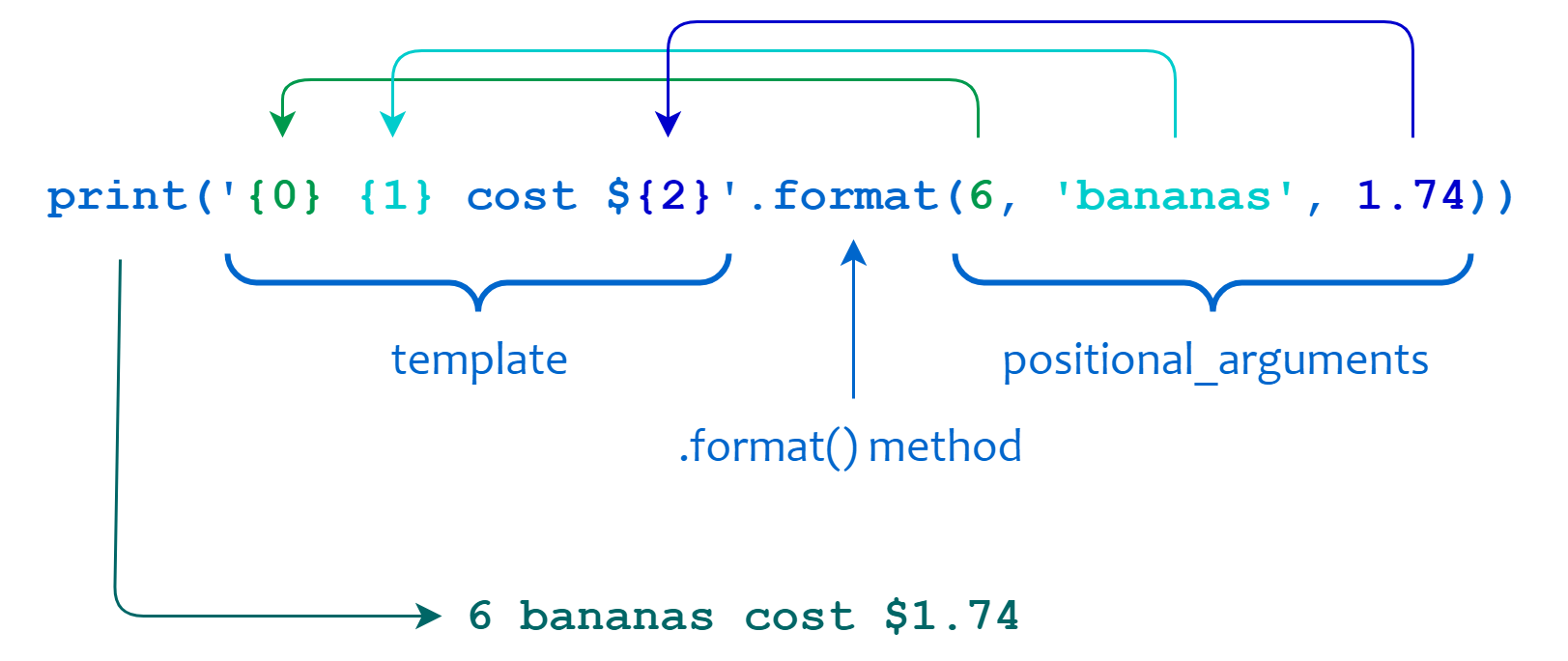
Python 3 #25: форматирование строк: метод format и F-строки

Python 3 #26: создание и импорт модулей — import, from, as, dir, reload

Python 3 #27: пакеты (package) — создание, импорт, установка (менеджер pip)

Python 3 #28: декораторы функций и замыкания

Python 3 #29: установка и порядок работы в PyCharm

Python 3 #30: функция enumerate, примеры использования

2 ответа

Лучший ответ

Согласованность .

Вам нужно будет следовать некоторым очень простым и, казалось бы, неуместным объяснениям, чтобы понять это.

В школе вы выучили деление с остатком. И вы сделали расчеты следующим образом:

Позже вы выучили деления на действительные числа:

До этого момента вы можете полагать, что и всегда дают один и тот же результат. Это ваше текущее понимание ситуации.

Однако посмотрите, что происходит в целочисленном делении: число за R циклически изменяется от 3, 2, 1 до 0, а затем перезапускается: 3, 2, 1, 0. Число перед R уменьшается с каждым 4-м шагом.

Итак, как это будет продолжаться?

В то же время деление действительных чисел дает нам:

Вот почему дает -1, а дает 0.

Ну, они служат различным целям: является частью вычисления целых чисел с остатками, а дает вам часть перед операции с действительным числом.

Вы решаете, что вы хотите вычислить, затем вы решаете, какой оператор использовать в Python, чтобы получить правильный результат.

Хороший вопрос. Продолжайте учиться.

61

Thomas Weller
12 Дек 2019 в 12:56

Я бы сказал, что ваше наблюдение о том, что эти 2 операции должны быть интуитивно схожими, ожидается, поскольку при положительных числах они ведут себя одинаково. Но если вы посмотрите на их происхождение (одно из математики, а другое — из информатики), тогда будет более понятно их различное поведение.

Вы можете посмотреть там концепции:

• Этажное деление или функция пола, применяемое к математическому разделению
• Тип преобразования / Тип литья

================================================== ================

I) Этажное деление или функция пола, применяемая к математическому разделу

Функция пола — очень хорошо зарекомендовавшая себя концепция математики.

Из mathworld.wolfram:

Таким образом, разделение по этажам — это не более, чем функция по этажам, применяемая к математическому разделению. Поведение очень ясное, «математически точное».

II) Преобразование типов / приведение типов

Из википедии:

В большинстве языков программирования приведение формы с плавающей точкой к целому числу применяется правилом округления (поэтому существует соглашение):

Округление к 0 — направленное округление к нулю (также известное как усечение)

Правило округления в соответствии с IEEE 754.

Итак, другими словами, причина различия между целочисленным делением и преобразованием с плавающей точкой в int в python является математической, вот некоторые мысли от Гвидо ван Россума (думаю, мне не нужно его представлять: D) (из блог История Python, статья «Почему Python Целочисленное деление этажей «)

4

rusu_ro1
7 Янв 2020 в 22:09

Тригонометрические функции в Python

Модуль math в Python поддерживает все тригонометрические функции. Самые популярные представлены ниже:

• : Возвращает синус в радианах;
• : Возвращает косинус в радианах;
• : Возвращает тангенс в радианах;
• : Возвращает инвертированный синус. Аналогичным образом работают и ;
• : Конвертирует угол из радиан в градусы;
• : Конвертирует угол из градусов в радианы.

Рассмотрим следующий пример:

Python

import math

angle_In_Degrees = 62
angle_In_Radians = math.radians(angle_In_Degrees)

print(‘Значение угла:’, angle_In_Radians)
print(‘sin(x) равен:’, math.sin(angle_In_Radians))
print(‘tan(x) равен:’, math.tan(angle_In_Radians))
print(‘cos(x) равен:’, math.cos(angle_In_Radians))

1 2 3 4 5 6 7 8 9

importmath angle_In_Degrees=62 angle_In_Radians=math.radians(angle_In_Degrees) print(‘Значение угла:’,angle_In_Radians) print(‘sin(x) равен:’,math.sin(angle_In_Radians)) print(‘tan(x) равен:’,math.tan(angle_In_Radians)) print(‘cos(x) равен:’,math.cos(angle_In_Radians))

Вывод

Shell

Значение угла: 1.0821041362364843
sin(x) равен: 0.8829475928589269
tan(x) равен: 1.8807264653463318
cos(x) равен: 0.46947156278589086

1 2 3 4

Значениеугла1.0821041362364843 sin(x)равен0.8829475928589269 tan(x)равен1.8807264653463318 cos(x)равен0.46947156278589086

Обратите внимание, что вначале мы конвертировали значение угла из градусов в радианы для осуществления дальнейших операций

Разделение строки с использованием разделителя

Python может разбивать строки по любому разделителю, указанному в качестве параметра метода . Таким разделителем может быть, например, запятая, точка или любой другой символ (или даже несколько символов).

Давайте рассмотрим пример, где в
качестве разделителя выступает запятая
и точка с запятой (это можно использовать
для работы с CSV-файлами).

print("Python2, Python3, Python, Numpy".split(','))
print("Python2; Python3; Python; Numpy".split(';'))

Результат:

Как видите, в результирующих списках
отсутствуют сами разделители.

Если вам нужно получить список, в
который войдут и разделители (в качестве
отдельных элементов), можно разбить
строку по шаблону, с использованием
регулярных выражений (см. ). Когда вы берете шаблон в
захватывающие круглые скобки, группа
в шаблоне также возвращается как часть
результирующего списка.

import re

sep = re.split(',', 'Python2, Python3, Python, Numpy')
print(sep)
sep = re.split('(,)', 'Python2, Python3, Python, Numpy')
print(sep)

Результат:

Если вы хотите, чтобы разделитель был частью каждой подстроки в списке, можно обойтись без регулярных выражений и использовать list comprehensions:

text = 'Python2, Python3, Python, Numpy'
sep = ','

result = 
print(result)

Результат:

Целые числа (int)

В Python любое число, состоящее из десятичных цифр без префикса, интерпретируется как десятичное число типа

Целые числа в Python представлены только одним типом – PyLongObject, реализация которого лежит в longobject.c, а сама структура выглядит так:

Любое целое число состоит из массива цифр переменной длины, поэтому в Python 3 в переменную типа может быть записано число неограниченной длины. Единственное ограничение длины – это размер оперативной памяти.

Целые числа могут записываться не только как десятичные, но и как двоичные, восьмеричные или шестнадцатеричные. Для этого перед числом нужно написать символы:

• 0b (0B) – для двоичного представления;
• 0o (0O) – для восьмеричного представления;
• 0x (0X) – для шестнадцатеричного представления.