Сортировка массива в python

Введение

Быстрая сортировка — популярный алгоритм сортировки, который часто используется вместе с сортировкой слиянием. Это алгоритм является хорошим примером эффективного алгоритма сортировки со средней сложностью O(n log_n). Часть его популярности еще связана с простотой реализации.

Быстрая сортировка является представителем трех типов алгоритмов: divide and conquer (разделяй и властвуй), in-place (на месте) и unstable (нестабильный).

• Divide and conquer: Быстрая сортировка разбивает массив на меньшие массивы до тех пор, пока он не закончится пустым массивом, или массивом, содержащим только один элемент, и затем все рекурсивно соединяется в сортированный большой массив.
• In place: Быстрая сортировка не создает никаких копий массива или его подмассивов. Однако этот алгоритм требует много стековой памяти для всех рекурсивных вызовов, которые он делает.
• Unstable: стабильный (stable) алгоритм сортировки — это алгоритм, в котором элементы с одинаковым значением отображаются в том же относительном порядке в отсортированном массиве, что и до сортировки массива. Нестабильный алгоритм сортировки не гарантирует этого, это, конечно, может случиться, но не гарантируется. Это может быть важным, когда вы сортируете объекты вместо примитивных типов. Например, представьте, что у вас есть несколько объектов Person одного и того же возраста, например, Дейва в возрасте 21 года и Майка в возрасте 21 года. Если бы вы использовали Quicksort в коллекции, содержащей Дейва и Майка, отсортированных по возрасту, нет гарантии, что Дейв будет приходить раньше Майка каждый раз, когда вы запускаете алгоритм, и наоборот.

Сравнение скоростей сортировок

Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.

Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.

Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.

Лучше понять эти алгоритмы вам поможет их визуализация.

Перевод статьи «Sorting Algorithms in Python»

sorted() With a key Argument

One of the most powerful components of is the keyword argument called . This argument expects a function to be passed to it, and that function will be used on each value in the list being sorted to determine the resulting order.

To demonstrate a basic example, let’s assume the requirement for ordering a specific list is the length of the strings in the list, shortest to longest. The function to return the length of a string, , will be used with the argument:

>>>

The resulting order is a list with a string order of shortest to longest. The length of each element in the list is determined by and then returned in ascending order.

Let’s return to the earlier example of sorting by first letter when the case is different. can be used to solve that problem by converting the entire string to lowercase:

>>>

The output values have not been converted to lowercase because does not manipulate the data in the original list. During sorting, the function passed to is being called on each element to determine sort order, but the original values will be in the output.

There are two main limitations when you’re using functions with the argument.

First, the number of required arguments in the function passed to must be one.

The example below shows the definition of an addition function that takes two arguments. When that function is used in on a list of numbers, it fails because it is missing a second argument. Each time is called during the sort, it is only receiving one element from the list at a time:

>>>

The second limitation is that the function used with must be able to handle all the values in the iterable. For example, you have a list of numbers represented as strings to be used in , and is going to attempt to convert them to numbers using . If a value in the iterable can’t be cast to an integer, then the function will fail:

>>>

Each numeric value as a can be converted to , but can’t. This causes a to be raised and explain that can’t be converted to because it is invalid.

The functionality is extremely powerful because almost any function, built-in or user-defined, can be used to manipulate the output order.

If the ordering requirement is to order an iterable by the last letter in each string (and if the letter is the same, then to use the next letter), then a function can be defined and then used in the sorting. The example below defines a function that reverses the string passed to it, and then that function is used as the argument for :

>>>

The slice syntax is used to reverse a string. Each element will have applied to it, and the sorting order will be based on the characters in the backwards word.

Instead of writing a standalone function, you can use a function defined in the argument.

A is an anonymous function that:

1. Must be defined inline
2. Doesn’t have a name
3. Can’t contain statements
4. Will execute just like a function

In the example below, the is defined as a with no name, the argument taken by the is , and is the operation that will be performed on the argument:

>>>

is called on each element and reverses the word. That reversed output is then used for sorting, but the original words are still returned.

If the requirement changes, and the order should be reversed as well, then the keyword can be used alongside the argument:

>>>

functions are also useful when you need to sort objects based on a property. If you have a group of students and need to sort them by their final grade, highest to lowest, then a can be used to get the property from the :

>>>

This example uses to produce classes with and attributes. The calls on each element and returns the value for .

is set to to make the ascending output flipped to be descending so that the highest grades are ordered first.

The possibilities are endless for how ordering can be done when you leverage both the and keyword arguments on . Code can be kept clean and short when you use a basic for a small function, or you can write a whole new function, import it, and use it in the key argument.

Если можно менять исходные списки

Предположим, что после слияния старые списки больше не нужны (как обычно и случается). Тогда можно написать еще один способ. Будем как и раньше сравнивать нулевые элементы списков и вызывать у списка с меньшим, пока один из списков не закончится.

Получили простенькую функцию на 4 строчки, но использовать дальше исходные списки не получится. Можно их скопировать, потом работать с копиями, но это потребует много дополнительного времени. Здесь будут проблемы с тем, что удаление нулевого элемента очень дорогое. Поэтому еще одна модификация будет заключаться в том, что мы будем вместо удаления из начала списка использовать удаление из конца, но придется в конце развернуть списки.

Odd and Ends

• For locale aware sorting, use locale.strxfrm() for a key function or locale.strcoll() for a comparison function.

• The reverse parameter still maintains sort stability (i.e. records with equal keys retain the original order). Interestingly, that effect can be simulated without the parameter by using the builtin reversed function twice:

  >>> data =
  >>> assert sorted(data, reverse=True) == list(reversed(sorted(reversed(data))))

• To create a standard sort order for a class, just add the appropriate rich comparison methods:

  >>> Student.__eq__ = lambda self, other: self.age == other.age
  >>> Student.__ne__ = lambda self, other: self.age != other.age
  >>> Student.__lt__ = lambda self, other: self.age >> Student.__le__ = lambda self, other: self.age >> Student.__gt__ = lambda self, other: self.age > other.age
  >>> Student.__ge__ = lambda self, other: self.age >= other.age
  >>> sorted(student_objects)

  For general purpose comparisons, the recommended approach is to define all six rich comparison operators. The functools.total_ordering class decorator makes this easy to implement.

• Key functions need not access data internal to objects being sorted. A key function can also access external resources. For instance, if the student grades are stored in a dictionary, they can be used to sort a separate list of student names:

  >>> students =
  >>> newgrades = {‘john’: ‘F’, ‘jane’:’A’, ‘dave’: ‘C’}
  >>> sorted(students, key=newgrades.__getitem__)

Своя сортирующая функция

Язык Python позволяет
создавать свои сортирующие функции для более точной настройки алгоритма
сортировки. Давайте для начала рассмотрим такой пример. Пусть у нас имеется вот
такой список:

a=1,4,3,6,5,2

и мы хотим,
чтобы вначале стояли четные элементы, а в конце – нечетные. Для этого создадим
такую вспомогательную функцию:

def funcSort(x):
    return x%2

И укажем ее при
сортировке:

print( sorted(a, key=funcSort) )

Мы здесь
используем именованный параметр key, который принимает ссылку на
сортирующую функцию. Запускаем программу и видим следующий результат:

Разберемся,
почему так произошло. Смотрите, функция funcSort возвращает вот
такие значения для каждого элемента списка a:

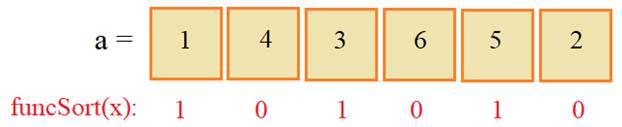
И, далее, в sorted уже
используются именно эти значения для сортировки элементов по возрастанию. То
есть, сначала, по порядку берется элемент со значением 4, затем, 6 и потом 2.
После этого следуют нечетные значения в порядке их следования: 1, 3, 5. В
результате мы получаем список:

А теперь,
давайте модифицируем нашу функцию, чтобы выполнялась сортировка и самих
значений:

def funcSort(x):
    if x%2 == :
        return x
    else:
        return x+100

Здесь четные
значения возвращаются такими как они есть, а к нечетным прибавляем 100. В
результате получим:

Здесь элементам
нашего списка ставятся в соответствие указанные числа, и по этим числам
выполняется их сортировка. То есть, эти числа можно воспринимать как некие
ключи, по которым и происходит сортировка элементов списка. Поэтому в Python
такую
сортировку называют сортировкой по ключам.

Конечно, здесь
вместо определения своей функции можно также записывать анонимные функции,
например:

print( sorted(a, key=lambda x: x%2) )

Получим ранее
рассмотренный результат:

Или, то же самое
можно делать и со строками:

lst = "Москва", "Тверь", "Смоленск", "Псков", "Рязань"

Отсортируем их
по длине строки:

print( sorted(lst, key=len) )

получим
результат:

Или по
последнему символу, используя лексикографический порядок:

print( sorted(lst, key=lambda x: x-1) )

Или, по первому
символу:

print( sorted(lst, key=lambda x: x) )

И так далее. Этот
подход часто используют при сортировке сложных структур данных. Допустим, у нас
имеется вот такой список из книг:

books = {
("Евгений Онегин", "Пушкин А.С.", 200),
("Муму", "Тургенев И.С.", 250),
("Мастер и Маргарита", "Булгаков М.А.", 500),
("Мертвые души", "Гоголь Н.В.", 190)
}

И нам нужно его
отсортировать по возрастанию цены (последнее значение). Это можно сделать так:

print( sorted(books, key=lambda x: x2) )

На выходе
получим список:

Вот так можно
выполнять сортировку данных в Python.

Использовать

Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя

Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение

Хотя пузырьковая сортировка является одним из простейших алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.

Из-за своей простоты пузырьковая сортировка часто используется для ознакомления с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.

Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковая сортировка, кажется, не имеет ничего, что могло бы ее рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.

Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в ​​худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.

Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .

В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.

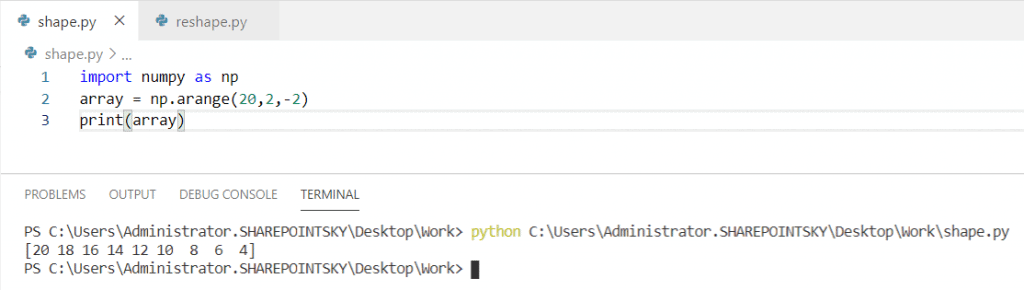
Массив нарезки

Все идет нормально; Создание и индексация массивов выглядит знакомо.

Теперь мы подошли к нарезке массивов, и это одна из функций, которая создает проблемы для начинающих массивов Python и NumPy.

Структуры, такие как списки и массивы NumPy, могут быть нарезаны. Это означает, что подпоследовательность структуры может быть проиндексирована и извлечена.

Это наиболее полезно при машинном обучении при указании входных и выходных переменных или разделении обучающих строк из строк тестирования.

Нарезка задается с помощью оператора двоеточия ‘:’ с ‘от’ а также ‘в‘Индекс до и после столбца соответственно. Срез начинается от индекса «от» и заканчивается на один элемент перед индексом «до».

Давайте рассмотрим несколько примеров.

Одномерная нарезка

Вы можете получить доступ ко всем данным в измерении массива, указав срез «:» без индексов.

При выполнении примера печатаются все элементы в массиве.

Первый элемент массива можно разрезать, указав фрагмент, который начинается с индекса 0 и заканчивается индексом 1 (один элемент перед индексом «до»)

Выполнение примера возвращает подмассив с первым элементом.

Мы также можем использовать отрицательные индексы в срезах. Например, мы можем нарезать последние два элемента в списке, начав срез с -2 (второй последний элемент) и не указав индекс «до»; это берет ломтик до конца измерения.

Выполнение примера возвращает подмассив только с двумя последними элементами.

Двумерная нарезка

Давайте рассмотрим два примера двумерного среза, которые вы, скорее всего, будете использовать в машинном обучении.

Разделение функций ввода и вывода

Распространено загруженные данные на входные переменные (X) и выходную переменную (y).

Мы можем сделать это, разрезая все строки и все столбцы до, но перед последним столбцом, затем отдельно индексируя последний столбец.

Для входных объектов мы можем выбрать все строки и все столбцы, кроме последнего, указав ‘:’ в индексе строк и: -1 в индексе столбцов.

Для выходного столбца мы можем снова выбрать все строки, используя ‘:’, и индексировать только последний столбец, указав индекс -1.

Собрав все это вместе, мы можем разделить 3-колоночный 2D-набор данных на входные и выходные данные следующим образом:

При выполнении примера печатаются разделенные элементы X и y

Обратите внимание, что X — это двумерный массив, а y — это одномерный массив

Сплит поезд и тестовые ряды

Обычно загруженный набор данных разбивают на отдельные наборы поездов и тестов.

Это разделение строк, где некоторая часть будет использоваться для обучения модели, а оставшаяся часть будет использоваться для оценки мастерства обученной модели.

Для этого потребуется разрезать все столбцы, указав «:» во втором индексе измерения. Набор обучающих данных будет содержать все строки от начала до точки разделения.

Тестовым набором данных будут все строки, начиная с точки разделения до конца измерения.

Собрав все это вместе, мы можем разделить набор данных в надуманной точке разделения 2.

При выполнении примера выбираются первые две строки для обучения и последняя строка для набора тестов.

Алгоритм быстрой сортировки

Этот алгоритм также использует разделяй и стратегию завоюйте, но использует подход сверху вниз вместо первого разделения массива вокруг шарнирного элемента (здесь, мы всегда выбираем последний элемент массива будут стержень).

Таким образом гарантируется, что после каждого шага точка поворота находится в назначенной позиции в окончательном отсортированном массиве.

Убедившись, что массив разделен вокруг оси поворота (элементы, меньшие точки поворота, находятся слева, а элементы, которые больше оси поворота, находятся справа), мы продолжаем применять функцию к остальной части, пока все элементы находятся в соответствующих позициях, когда массив полностью отсортирован.

def quicksort(a, arr_type):
    def do_partition(a, arr_type, start, end):
        # Performs the partitioning of the subarray a
        
        # We choose the last element as the pivot
        pivot_idx = end
        pivot = a

        # Keep an index for the first partition
        # subarray (elements lesser than the pivot element)
        idx = start - 1

        def increment_and_swap(j):
            nonlocal idx
            idx += 1
            a, a = a, a

         < pivot]
        
        # Finally, we need to swap the pivot (a with a)
        # since we have reached the position of the pivot in the actual
        # sorted array
        a, a = a, a

        # Return the final updated position of the pivot
        # after partitioning
        return idx+1

    def quicksort_helper(a, arr_type, start, end):
        if start < end:
            # Do the partitioning first and then go via
            # a top down divide and conquer, as opposed
            # to the bottom up mergesort
            pivot_idx = do_partition(a, arr_type, start, end)
            quicksort_helper(a, arr_type, start, pivot_idx-1)
            quicksort_helper(a, arr_type, pivot_idx+1, end)

    quicksort_helper(a, arr_type, 0, len(a)-1)

Здесь метод выполняет шаг подхода Divide and Conquer, в то время метод разделяет массив вокруг точки поворота и возвращает позицию точки поворота, вокруг которой мы продолжаем рекурсивно разбивать подмассив до и после точки поворота, пока не будет весь массив отсортирован.

Прецедент:

b = array.array('i', )
print('Before QuickSort ->', b)
quicksort(b, 'i')
print('After QuickSort ->', b)

Вывод:

Before QuickSort -> array('i', )
After QuickSort -> array('i', )

Сортировка слиянием

Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.

Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.

Алгоритм

Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.

Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.

Реализация

Обратите внимание, что функция , в отличие от предыдущих алгоритмов, возвращает новый список, а не сортирует существующий. Поэтому такая сортировка требует больше памяти для создания нового списка того же размера, что и входной список

Параметр key

Функций и sorted() содержат параметр key чтобы указать функцию вызываемую для каждого аргумента перед сравнением.

Пример регистронезависимого сравнения:

>>> sorted(«This is a test string from Andrew».split(), key=str.lower)

1 2	>>>sorted(«This is a test string from Andrew».split(),key=str.lower) ‘a’,’Andrew’,’from’,’is’,’string’,’test’,’This’

Функция передаваемая в key содержит один аргумент и возвращает ключ используемый для сортировки. Это эффективный подход, так как функция вызывается ровно один раз для каждого элемента.

Общий шаблон для отсортировки сложных объектов — использование одного из индексов как ключа:

>>> student_tuples =
>>> sorted(student_tuples, key=lambda student: student) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_tuples= …(‘john’,’A’,15), …(‘jane’,’B’,12), …(‘dave’,’B’,10), >>>sorted(student_tuples,key=lambda studentstudent2)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Тот же способ работает для объектов с именованными атрибутам:

>>> class Student:
… def __init__(self, name, grade, age):
… self.name = name
… self.grade = grade
… self.age = age
… def __repr__(self):
… return repr((self.name, self.grade, self.age))

1 2 3 4 5 6 7

>>>classStudent …def __init__(self,name,grade,age) …self.name=name …self.grade=grade …self.age=age …def __repr__(self) …returnrepr((self.name,self.grade,self.age))

>>> student_objects =
>>> sorted(student_objects, key=lambda student: student.age) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_objects= …Student(‘john’,’A’,15), …Student(‘jane’,’B’,12), …Student(‘dave’,’B’,10), >>>sorted(student_objects,key=lambda studentstudent.age)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Operator Module Functions

The key-function patterns shown above are very common, so Python provides convenience functions to make accessor functions easier and faster. The has itemgetter, attrgetter, and starting in Python 2.6 a methodcaller function.

Using those functions, the above examples become simpler and faster.

>>> from operator import itemgetter, attrgetter, methodcaller

>>> sorted(student_tuples, key=itemgetter(2))


>>> sorted(student_objects, key=attrgetter('age'))

The operator module functions allow multiple levels of sorting. For example, to sort by grade then by age:

>>> sorted(student_tuples, key=itemgetter(1,2))


>>> sorted(student_objects, key=attrgetter('grade', 'age'))

The third function from the operator module, methodcaller is used in the following example in which the weighted grade of each student is shown before sorting on it:

>>> 

>>> sorted(student_objects, key=methodcaller('weighted_grade'))