Визуализации алгоритмов сортировки
Содержание:
Analysis
There are outer iterations needed to sort the array, because every iteration puts one element to it’s place. Every inner iteration needs one step less the previous one, since the problem size is gradually decreasing.
Last part of the algorithm is a condition, which decides whether we should swap the adjacent elements.
Complexity
The complexity of the condition (and possible swap) is obviously constant (). The inner cycle will be performed
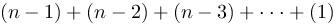
times.
Which is in total (according to the formula for arithmetic sequence):
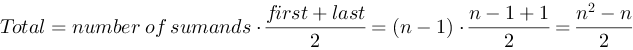
Because this number represents the best and the worst case of algorithm behavior, it’s asymptotic complexity after omitting additive and multiplicative constants is .
Использовать
Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя
Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение
Хотя пузырьковая сортировка является одним из простейших алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.
Из-за своей простоты пузырьковая сортировка часто используется для ознакомления с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.
Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковая сортировка, кажется, не имеет ничего, что могло бы ее рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.
Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.
Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .
В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.
Modified Bubble Sort
Bubble sort complexities remain o(n2) is all cases including sorted array. We can reduce the time complexity to O(n) if the array is already sorted.Also,we need to introduce a flag variable to stop the bubble sort as soon as it becomes sorted.
The flag variable is initialized as true in every iteration and in for loop if array goes in for swapping we will initialize it to false. But if no swapping takes place in the inner loop then its value will remain true and we will have an if condition after the nested loop that will check the flag value and if flag value remains true, we will break
Modified Bubble Sort Time Complexity
- Best Time Complexity : O(n), i.e when the elements in the given array are sorted.So, only once the every element is accessed or traversed.
- Average Time Complexity : O(n^2)
- Worst Time Complexity : O(n^2)
Bubble Sort — Explanation
In the first “pass” through the array, the largest element will always get swapped until it is placed to the extreme right. This is because this largest element will always break the desired order. So, at the end of the first pass, the largest element will always reach its correct position.
Now that the largest element has reached its correct position (for instance, 5 reached the last position), we can simply ignore it and concentrate on the rest of the array ( in the above case). Here, the largest element in the rest of the array (which is 4) will be nothing but the second largest element in the array. By the above recursive argument, this second largest array will then reach the last position in the remaining array (). This is nothing but a recursive argument on the remaining array.
This continues until for n iterations where n = number of elements in the array. Finally, the array gets sorted.
#include <stdio.h>void bubble_sort(int a[], int n) { int i = 0, j = 0, tmp; for (i = 0; i < n; i++) { // loop n times - 1 per element for (j = 0; j < n - i - 1; j++) { // last i elements are sorted already if (a > a) { // swop if order is broken tmp = a; a = a; a = tmp; } } }}int main() { int a, n, i, d, swap; printf("Enter number of elements in the array:\n"); scanf("%d", &n); printf("Enter %d integers\n", n); for (i = 0; i < n; i++) scanf("%d", &a); bubble_sort(a, n); printf("Printing the sorted array:\n"); for (i = 0; i < n; i++) printf("%d\n", a); return 0;}
Подробный разбор пузырьковой сортировки
Давайте разберем подробно как работает пузырьковая сортировка
Первая итереация (первый повтор алгоритма) меняет между собой 4 и 2 так как цифра два меньше чем четыре 2<4, повторюсь что алгоритм меняет значения между собой если, слева оно меньше чем справа. Далее происходит сверка между 4 и 3, и так как 3 меньше чем 4 (3<4) происходит обмен значениями. Потом проходит проверку между 4 и 8 и так как значение 4 меньше чем 8 то не происходит обмена, ведь уже и так всё на своих местах.
Далее сравнивается 8 и 1 и так как 1 меньше чем 8 (1<8) и оно не находиться слева то происходит обмен значениями.После это первый повтор алгоритма заканчивается, на анимации я выделил это зеленым фоном.
В итоге по окончанию работы алгоритма пузырьковой сортировки мы имеем следующий порядок числового массива: 2 3 4 1 8

и начинается второй повтор алгоритма.
Далее сравнивается 2 и 3 и так как два меньше чем три и оно находиться слева то просто идем дальше ничего не трогая. Также проверяем и 3 и 4 и тоже самое условие выполняется 3<4 и оно слева. Дальше проверяется 4 и 1 и тут мы видим что число 1<4 и не находиться слева, поэтому алгоритм меняет их местами. В крайний раз для второго повторения алгоритма проверяется 4 и 8, но тут всё в порядке, и мы дошли до конца начинаем третье повторение. Итоги для второго повторения такие : 2 3 1 4 8

Третье повторение пузырькового алгоритма начинается с сравнения 2 и 3, тут алгоритм проверяет что 2<3 и 2 находиться слева и оставляет их в покое и идет дальше. Сравнение же 3 и 1 показывает что 1 то меньше чем три, но почему то не слева и меняет их местами. Далее идет сравнение 3 и 4, тут всё в порядке и так далее до сравнения 4 и 8.
После этого получается следующий результат: 2 1 3 4 8

Как мы видим почти все цифры уже на своих местах и в порядке возрастания! Осталось только в последнем повторении пузырькового алгоритма поменять местами 2 и 1 и всё. После того как алгоритм закончил свою работу и проверил что цифры больше нельзя поменять местами он перестает работать с таким вот результатом: 1 2 3 4 8

Сортировка массива из случайных чисел методом пузырька
Массив называется отсортированным по возрастанию, если для любых его элементов выполняется
условие a<a. Массив называется отсортированным по убыванию, если для любых его элементов выполняется условие a>a.
Существует множество методов сортировки. Одни из них являются более эффективными, другие
проще для понимания. Достаточно простой для понимания является сортировка методом пузырька, который
также называют методом простого обмена. В чем же он заключается, и почему у него такое странное
название: «метод пузырька»?
Как известно воздух легче воды, поэтому пузырьки воздуха всплывают. Это просто аналогия. В
сортировке методом пузырька по возрастанию более легкие (с меньшим значением) элементы постепенно
«всплывают» в начало массива, а более тяжелые друг за другом опускаются на дно (в конец массива).
Алгоритм и особенности сортировки:
- При первом проходе по массиву элементы попарно сравниваются между собой: первый со вторым, затем второй с третьим, следом третий с четвертым и т.д. Если предшествующий элемент оказывается больше последующего, то их меняют местами.
- Не трудно догадаться, что постепенно самое большое число оказывается последним. Остальная часть массива остается не отсортированной, хотя некоторое перемещение элементов с меньшим значением в начало массива наблюдается.
- При втором проходе незачем сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте. Значит, число сравнений будет на одно меньше.
- На третьем проходе уже не надо сравнивать предпоследний и третий элемент с конца. Поэтому число сравнений будет на два меньше, чем при первом проходе.
- В конце концов, при проходе по массиву, когда остаются только два элемента, которые надо сравнить, выполняется только одно сравнение.
- После этого первый элемент не с чем сравнивать, и, следовательно, последний проход по массиву не нужен. Другими словами, количество проходов по массиву равно n-1, где n – это количество элементов массива.
- Количество сравнений в каждом проходе равно n-j, где j – это номер прохода по массиву (первый, второй, третий и т.д.).
- При обмене элементов массива обычно используется «буферная» (третья) переменная, куда временно помещается значение одного из элементов.
Delphi/Pascal
const
n = 10; { количество элементов в массиве }
var
a:array of integer;
i,j,buf:integer;
begin
{Заполняем массив случайными целыми числами от 0 до 50 и выводим массив на экран}
for i:=1 to n do
begin
a:=random(50);
write(a:3);
end;
{ сортировка массива по возрастанию }
for j:=1 to n-1 do
for i:= 1 to n-j do {проверяем все элементы до предпоследнего неотсортированного}
if a>a then { ищем элементы, которые стоят неправильно }
begin { меняем элементы местами }
buf:=a;
a:=a;
a:=buf;
end;
writeln;
writeln(‘Массив после сортировки: ‘);
for i:=1 to n do write(a,’ ‘);
end.
|
1 |
const n=10;{количествоэлементоввмассиве} var aarray1..nofinteger; i,j,bufinteger; begin {Заполняеммассивслучайнымицелымичисламиотдо50ивыводиммассивнаэкран} fori:=1tondo begin ai=random(50); write(ai3); end; {сортировкамассиваповозрастанию} forj:=1ton-1do fori=1ton-jdo{проверяемвсеэлементыдопредпоследнегонеотсортированного} ifai>ai+1then{ищемэлементы,которыестоятнеправильно} begin{меняемэлементыместами} buf:=ai; ai=ai+1; ai+1=buf; end; writeln; writeln(‘Массив после сортировки: ‘); fori:=1tondowrite(ai,’ ‘); end. |
Количество просмотров: 4 653
| Категория: Pascal | Тэги: сортировка
Параметр key
Функций и sorted() содержат параметр key чтобы указать функцию вызываемую для каждого аргумента перед сравнением.
Пример регистронезависимого сравнения:
>>> sorted(«This is a test string from Andrew».split(), key=str.lower)
|
1 |
>>>sorted(«This is a test string from Andrew».split(),key=str.lower) ‘a’,’Andrew’,’from’,’is’,’string’,’test’,’This’ |
Функция передаваемая в key содержит один аргумент и возвращает ключ используемый для сортировки. Это эффективный подход, так как функция вызывается ровно один раз для каждого элемента.
Общий шаблон для отсортировки сложных объектов — использование одного из индексов как ключа:
>>> student_tuples =
>>> sorted(student_tuples, key=lambda student: student) # сортировка по возрасту
|
1 |
>>>student_tuples= …(‘john’,’A’,15), …(‘jane’,’B’,12), …(‘dave’,’B’,10), >>>sorted(student_tuples,key=lambda studentstudent2)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15) |
Тот же способ работает для объектов с именованными атрибутам:
>>> class Student:
… def __init__(self, name, grade, age):
… self.name = name
… self.grade = grade
… self.age = age
… def __repr__(self):
… return repr((self.name, self.grade, self.age))
|
1 |
>>>classStudent …def __init__(self,name,grade,age) …self.name=name …self.grade=grade …self.age=age …def __repr__(self) …returnrepr((self.name,self.grade,self.age)) |
>>> student_objects =
>>> sorted(student_objects, key=lambda student: student.age) # сортировка по возрасту
|
1 |
>>>student_objects= …Student(‘john’,’A’,15), …Student(‘jane’,’B’,12), …Student(‘dave’,’B’,10), >>>sorted(student_objects,key=lambda studentstudent.age)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15) |
Разница между пузырьковой сортировкой и выборочной сортировкой
Определение
Bubble sort — простой алгоритм сортировки, который непрерывно проходит по списку и сравнивает соседние пары для сортировки элементов. Напротив, сортировка выбора — это алгоритм сортировки, который принимает наименьшее значение (с учетом возрастания) в списке и перемещает его в нужную позицию в массиве. Таким образом, в этом заключается основное различие между сортировкой пузырьков и сортировкой выбора.
функциональность
Пузырьковая сортировка сравнивает соседние элементы и соответственно меняет местами, в то время как сортировка выбора выбирает минимальный элемент из несортированного подмассива и помещает его в следующую позицию отсортированного подмассива.
КПД
Кроме того, еще одно различие между сортировкой пузырьков и сортировкой выбора заключается в том, что сортировка выбора эффективна по сравнению с сортировкой пузырьков.
скорость
Кроме того, скорость является еще одной разницей между сортировкой пузырьков и сортировкой выбора. Сортировка выбора происходит быстрее по сравнению с пузырьковой сортировкой.
метод
Кроме того, еще одно различие между пузырьковой сортировкой и сортировкой выбора заключается в том, что в пузырьковой сортировке используется обмен элементов, а в выборочной сортировке используется выбор элементов.
Заключение
Таким образом, основное различие между сортировкой пузырьков и сортировкой выбора заключается в том, что сортировка пузырьков выполняется путем многократной замены смежных элементов, если они находятся в неправильном порядке. Напротив, сортировка выбора сортирует массив путем многократного нахождения минимального элемента из несортированной части и размещения его в начале массива.
Реализация сортировки вставки
Реализация алгоритма сортировки вставки в языке программирования Python.
Выход:
Объяснение:
В приведенном выше коде python у нас есть список, содержащий 10 несортированных чисел для сортировки. В первом цикле while мы выполняем итерацию от 2-го элемента так, чтобы первый элемент списка стал первым элементом отсортированного списка. Первый цикл while выбирает элемент из несортированного списка, а второй цикл while (вложенный в первый) сравнивает его с элементами отсортированного списка, если выбранный элемент меньше соседнего левого элемента (отсортированной части), то левый элемент сдвигается на место текущего элемента и текущий элемент копируется на место левого элемента. Последний цикл while, наконец, отображает отсортированный список.
Анализ Сложности
Из псевдокода и приведенной выше иллюстрации следует, что сортировка вставки является эффективным алгоритмом по сравнению с пузырьковой сортировкой или сортировкой выбора. Вместо использования цикла for и текущих условий он использует цикл while, который больше не выполняет никаких дополнительных шагов при сортировке списка.
Однако, даже если мы передадим сортированный список методу сортировки вставки, он все равно выполнит внешний цикл for, тем самым требуя n шагов для сортировки уже отсортированного списка. Это делает наилучшую временную сложность сортировки вставки линейной функцией N, где N-количество элементов в списке .
Таким образом, различные сложности для метода сортировки вставки приведены ниже:
| Таким образом, различные сложности для метода сортировки вставки приведены ниже: | O(n2) |
| В лучшем случае временная сложность | O(n) |
| Средняя временная сложность | O(n2) |
| Сложность пространства | O(1) |
Несмотря на эти сложности, мы все еще можем сделать вывод, что сортировка вставки является наиболее эффективным алгоритмом по сравнению с другими методами сортировки, такими как Пузырьковая сортировка и сортировка выбора.
Модификации[править]
Сортировка чет-нечетправить
Сортировка чет-нечет (англ. odd-even sort) — модификация пузырьковой сортировки, основанная на сравнении элементов стоящих на четных и нечетных позициях независимо друг от друга. Сложность — .
Псевдокод указан ниже:
function oddEvenSort(a):
for i = 0 to n - 1
if i mod 2 == 0
for j = 2 to n - 1 step 2
if a < a
swap(a, a)
else
for j = 1 to n - 1 step 2
if a < a
swap(a, a)
Преимущество этой сортировки — на нескольких процессорах она выполняется быстрее, так как четные и нечетные индексы сортируются параллельно.
Сортировка расческойправить
Сортировка расческой (англ. comb sort) — модификация пузырьковой сортировки, основанной на сравнении элементов на расстоянии. Сложность — , но стремится к . Является самой быстрой квадратичной сортировкой. Недостаток — она неустойчива. Псевдокод указан ниже:
function combSort(a):
k = 1.3
jump = n
bool swapped = true
while jump > 1 and swapped
if jump > 1
jump /= k
swapped = false
for i = 0 to size - jump - 1
if a < a
swap(a, a)
swapped = true
Пояснения: Изначально расстояние между сравниваемыми элементами равно , где — оптимальное число для этого алгоритма. Сортируем массив по этому расстоянию, потом уменьшаем его по этому же правилу. Когда расстояние между сравниваемыми элементами достигает единицы, массив досортировывается обычным пузырьком.
Сортировка перемешиваниемправить
Сортировка перемешиванием (англ. cocktail sort), также известная как Шейкерная сортировка — разновидность пузырьковой сортировки, сортирующая массив в двух направлениях на каждой итерации. В среднем, сортировка перемешиванием работает в два раза быстрее пузырька. Сложность — , но стремится она к , где — максимальное расстояние элемента в неотсортированном массиве от его позиции в отсортированном массиве. Псевдокод указан ниже:
function shakerSort(a):
begin = -1
end = n - 2
while swapped
swapped = false
begin++
for i = begin to end
if a > a
swap(a, a)
swapped = true
if !swapped
break
swapped = false
end--
for i = end downto begin
if a > a
swap(a, a)
swapped = true
Анализ
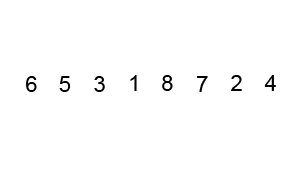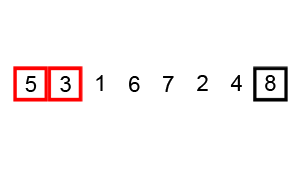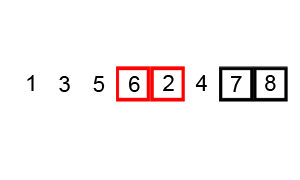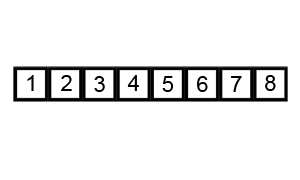
Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации необходимо сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.
Представление
Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n log n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.
Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (имеет небольшое количество инверсий ). Кроме того, если такое поведение желательно, его можно тривиально добавить к любому другому алгоритму, проверив список перед запуском алгоритма.
В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.
Кролики и черепахи
Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен двигаться к концу списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может двигаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n −1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .
Были предприняты различные попытки уничтожить черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам, чтобы сгладить список. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .
Пошаговый пример
Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему, используя пузырьковую сортировку. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;
- Первый проход
- ( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.
- (1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4
- (1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2
- (1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже упорядочены (8> 5), алгоритм не меняет их местами.
- Второй проход
- ( 1 4 2 5 8) → ( 1 4 2 5 8)
- (1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8 ) → (1 2 4 5 8 )
Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритму требуется один дополнительный полный проход без какой-либо подкачки, чтобы знать, что он отсортирован.
- Третий проход
- ( 1 2 4 5 8) → ( 1 2 4 5 8)
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8) → (1 2 4 5 8)
- (1 2 4 5 8 ) → (1 2 4 5 8 )