Excel поиск решения

Как добавить ограничения?

Если вам требуется добавить какие-то ограничения, то необходимо использовать кнопку «Добавить». Учтите, что при задании таких значений нужно быть предельно внимательным

Так как в Excel «Поиск решения» (примеры для которого мы рассматриваем) используется в достаточно ответственных операциях, чрезвычайно важно получать максимально правильные значения

Кстати, именно от ограничений эти самые результаты и зависят. Имейте в виду, что задавать их можно не только для каких-то отдельных ячеек, но и для целых их диапазонов. Какие варианты знаков и формул можно при этом использовать?

Вами могут применяться знаки: «=», «>=», «

Важно! Последний вариант допускает использование всех разных значений. Это доступно только в версиях Ексель 2010 и выше, что является еще одной причиной перехода именно на них. В этих пакетах офисного ПО «поиск оптимального» решения в Excel выполняется не только быстрее, но и куда качественнее

В этих пакетах офисного ПО «поиск оптимального» решения в Excel выполняется не только быстрее, но и куда качественнее.

Если мы говорим о расчете премии, то коэффициент должен быть строго положительным. Задать данный параметр можно сразу несколькими методами. Легко выполнить эту операцию, воспользовавшись кнопкой «Добавить». Кроме того, можно выставить флажок «Сделать переменные без ограничений неотрицательными». Где найти эту опцию в старых версиях программы?

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):
Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Решение задачи теории игр в Эксель, Excel

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием. Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Решение производственной задачи, Excel

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Решение общей задачи линейного программирования в Excel, Excel

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5. Для решения задачи используется ППП Excel.

Задача о продаже кондитерских изделий, Excel

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Задача сетевой оптимизации в Эксель, Excel

Решаем задачи вручную и в Excel с отчетом

Узнайте цену помощи

— Как быстро найти решение проблемы.

______

1) Дерево принятия решений.
Инструмент, поддерживающий принятие решений. Чаще всего он применяется при анализе данных и в статистике, но может использоваться и в обычной жизни. Дерево решений имеет «ствол», «ветки» и «листья». Ствол – это проблема, на ветках отображаются ее атрибуты, а на листьях – из значения. Среди достоинств метода следует выделить простоту его понимания и интерпретации, отсутствие необходимости в подготовке данных, возможность работать с интервалами и категориями, возможность оценки при помощи статических тестов, надежность и возможность обрабатывать большие потоки информации без подготовительных процедур.

2) Метод «Колесо».
Позволяет относительно быстро найти решение проблемы и произвести его оценку. Состоит из восьми шагов: сначала во всех деталях описывается проблемная ситуация, затем осуществляется поиск конкретных фактов и устанавливается недостающая информация, после этого проблема формулируется в позитивном ключе. Далее проводится мозговой штурм для создания поля идей для решения проблемы, производится оценка найденных вариантов на реалистичность, продумывается сценарий практического осуществления, составляется подробный план действий. На последнем этапе выполняются действия, после чего оценивается их эффективность.

Вас может заинтересовать статья «Алгоритм решения проблем«.

3) Метод «Три сундука».
Предназначен для еще более быстрого поиска решений проблем. В процессе необходимо наполнить информацией три «сундука». В первый кладутся ответы на вопрос: «Какие негативные последствия ждут нас, если мы пойдем по этому пути?». Для наполнения второго оценивается реальная угроза рисков, содержащихся в первом сундуке. Третий сундук наполняется возможными «противоядиями» от угроз второго сундука, которые находятся методом мозгового штурма. В результате находятся решения, реализуются на практике и оцениваются.

4) Метод последовательных приближений.
По сути, это метод проб и ошибок. Предпочтительно применять его тогда, когда мало информации по проблеме. Суть состоит в том, что последовательно выдвигаются и рассматриваются варианты решений. Неудачные идеи отбрасываются, а вместо них предлагаются новые, и опять проверяются. Никаких особых правил для поиска и оценки здесь нет – все решается субъективно, а эффективность метода зависит от того, насколько разбираются в вопросе люди (или человек), решающие проблему

При использовании метода важно учитывать элемент случайности

5) Матрица идей Буша.
Это метод анализа проблемных ситуаций и определения поля поиска решений. Чтобы его реализовать, нужно построить матрицу двусторонних отношений, для чего нужно ответить на вопросы: «Что?», «Кто?», «Где?», «Как?», «Зачем?», «Чем?» и «Когда?». Отвечая на них, человек получает всю информацию о проблеме. Если же вопросы скомбинировать, можно получить большую эвристическую подсказку для решения.

6) Матрица Эйзенхауэра.
Популярнейший инструмент поиска решений, применяемый обычными людьми и специалистами по всему миру

Смысл матрицы в том, чтобы научить человека оптимально распределять нагрузку, отличать важное и срочное, сокращать время на бессмысленные занятия. Матрица представляет собой четыре квадранта с двумя осями – важностью и срочностью

В каждый из них заносятся дела и задачи, и в результате человек получает объективную картину приоритетных задач.

7) Квадрат Декарта.
Очень простая техника принятия решений, на применение которой уходит совсем немного времени. Техника помогает выявить основные критерии выбора и дать оценку последствиям принимаемых решений. Для использования техники нужно нарисовать квадрат и разделить его на четыре части. В каждой части пишется вопрос: «Что будет, если это случится?», «Что будет, если этого не случится?», «Чего не будет, если это случится?» и «Чего не будет, если это не случится?». Эти вопросы являются пунктами наблюдения за проблемой. Именно с этих позиций и нужно ее рассматривать. Ответив на все вопросы, человек получает объективную картину положения дел и возможность оценить перспективы.

______

В чем важность пакетов ПО для офиса?

Любое ПО для офиса – это удобный инструмент, созданный для работы с большими базами данных, количество вспомогательных элементов в которых значительно увеличилось. Теперь с помощью средств визуализации, которые появились в новых версиях таких программ, работать стало куда легче. Появился новый фильтр поиска, значительно ускоряющий работу с большим потоком информации. Да и сам Microsoft Excel 2010 работает намного быстрее.

Казалось бы, совсем еще недавно секретарши осваивали премудрости MS Office 2007, как состоялся триумфальный релиз Office 2010, который добавил несчастным головной боли. Но не следует считать, что новая версия программы «подкидывает» своим пользователям только лишь сложности.

Пример тому — «поиск решения» в Excel 2010. Эта надстройка не только полезна, но и помогает сделать вашу работу с табличным редактором куда продуктивнее, позволяя решать намного более сложные задачи. Особенно он удобен для оптимизации, которая актуальна для многих современных компаний.

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

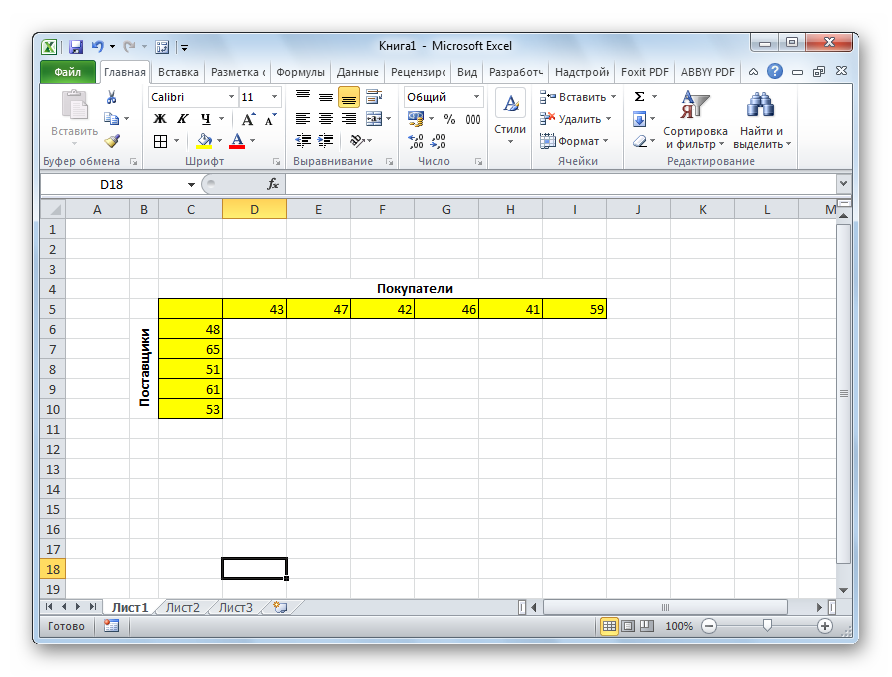
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.

Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.

Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».

Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».

Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».

Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.

Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».

Копируем маркером заполнения формулу на всю строку.

Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».

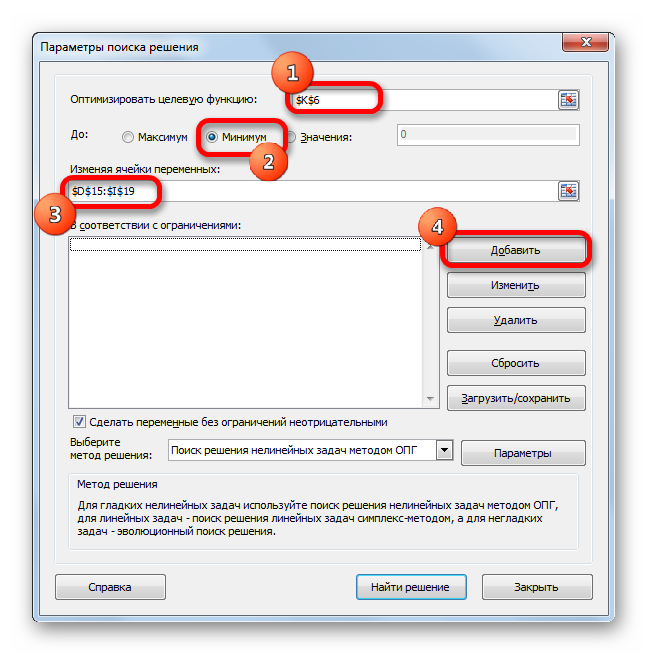
Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.

Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».

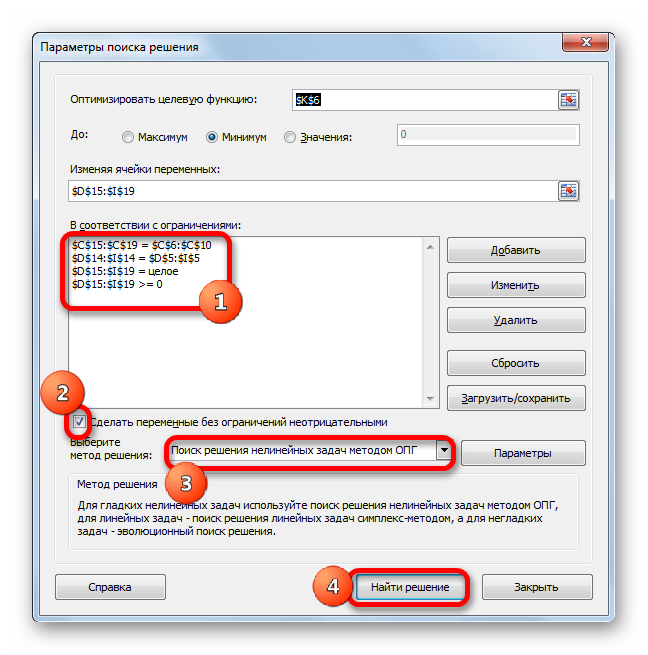
Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».

После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Установка Поиска решения

Команда Поиск решения находится в группе Анализ на вкладке Данные.

Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:

• На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки;
• В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
• В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

Примечание. Окно Надстройки также доступно на вкладке Разработчик. Как включить эту вкладку читайте здесь.

После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно.

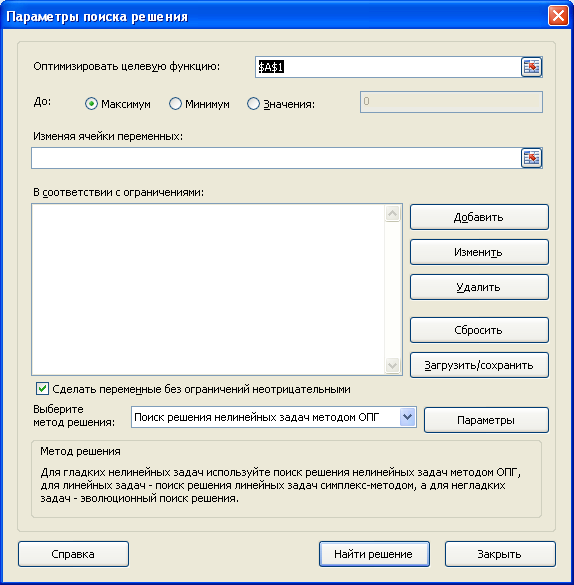
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа.

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет. Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка Поиск решения помогает определить лучший способ сделать что-то:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить план производства, при котором доход от реализации произведенной продукции максимальный;
• Определить схему перевозок, при которой общие затраты на перевозку были бы минимальными;
• Найти распределение нескольких станков по разным видам работ, чтобы общие затраты на производство продукции были бы минимальными;
• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра. Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра. Основные отличия Подбора параметра от Поиска решения:

• Подбор параметра работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Поиск решения в Excel

Поиск решения – это надстройка Excel, позволяющая делать задачи на оптимизацию. Как это работает: у вас есть данные, которые связаны между собой формулами. При этом на какой-то результирующий итог влияют как положительным, так и отрицательным образом. Например, прибыль зависит от расходов на рекламу как положительно (ведь чем больше рекламы, тем больше объем продаж), так и отрицательно (расходы на рекламу увеличивают общие расходы и уменьшают прибыль). В конце статьи будет ссылка на файл, где вы сможете сами посмотреть наглядно таблицу и прорешать параллельно со мной.

Поиск решения путем подбора данных находит наиболее эффективное значение. В нашем случае, максимальную прибыль. Я взял небольшую таблицу: Здесь, как видите, синим обозначена целевая ячейка, та, которую нужно максимизировать, изменяя расходы на рекламу (зеленые ячейки). Хитрость в том, что прибыль зависит от объема продаж (в штуках), а от него, в свою очередь зависят и расходы и доходы, которые формируют прибыль. Т.е., просто увеличив или уменьшив расходы на рекламу, вы не получите лучшего результата. В этом и состоит ценность Поиска решения – он делает перебор всех возможных значений по своему алгоритму и получает наилучший результат. Кто проходил обучение по моему самоучителю , уже в курсе, как это делается и как применяется.

Еще есть ограничение бюджет рекламных расходов в 40 тыс. долл. за 4 месяца.

Итак, приступим к технической части.

1. Если вы никогда не пользовались этой надстройкой, придется ее сначала установить. Дело в том, что по умолчанию Поиск решения не ставится. Заходим Офис/Параметры Excel/Надстройки/Кнопка “Перейти”. Мы уже заходили сюда, когда делали сумму прописью .
2. Теперь, у вас на вкладке Данные появилась команда “Поиск решения”. Нажимаем и видим такое окошко:
3. Целевая ячейка – это там, которую мы хотим максимизировать, это результат. У нас это B15. Т.е. я хочу увидеть, какими должны быть расходы на рекламу, чтобы в январе у меня была максимальная прибыль. Ставим выбор “максимальному значению”.
4. Изменяя ячейки – ставим диапазон ячеек, от которых зависит итог. У меня это все расходы на рекламу, т.е. диапазон B11 – E11.
5. Ограничения – ну без них никак. Excel мыслит больше математически, поэтому нам надо:

• Поставить условия положительности изменяемых ячеек. B11:E11 > 0
• Ограничить рекламный бюджет за 4 месяца. F11=40000

1. Нажимаем на кнопку “Выполнить”. Если что-то пошло не так, а это бывает, обнулите диапазон изменяемых ячеек, может помочь.

В итоге мы получим нужный результат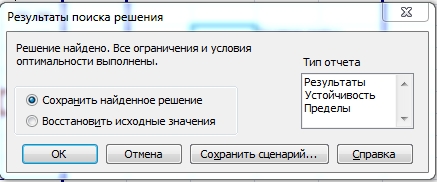

Если не получим, значит, надо пересмотреть условия, возможно, что-то некорректно проставлено или задача не имеет решения.

Видео по теме (5 минут):