Как округлить до десятых
Содержание:
- Как грамотно округлить число в Excel
- Правила округления десятичной дроби
- Способ 1: Функция «Увеличить разрядность»
- Ошибки Excel при округлении и введении данных в ячейки
- Примеры
- Ошибки округления и модуль decimal
- Способы округления чисел
- Округление натуральных чисел
- Как округлить число в Excel до целых, десятых, сотых в большую или меньшую сторону, формула округления, как убрать округление
- Работа с таблицами Excel
- Округление результатов вычислений
- Зачем нужно округление
- Работа с целыми цифрами
- Округление чисел
- Приближённые значения
Как грамотно округлить число в Excel
В нашем случае округление было осуществлено в сторону увеличения. Это зависит от числа, которое убирается. Если перед нужным значением находится 5 или больше, то округление осуществляется в направлении увеличения, а если меньше – уменьшения. Все так, как нужно делать в математике, никаких изменений в правилах нет.
Точность результата зависит от того, сколько знаков в дробной части человек решил оставить. Чем оно больше, тем выше точность. Поэтому настоятельно рекомендуется выполнять округление значений лишь в тех ситуациях, когда в этом есть реальная практическая необходимость. Иногда даже малейшее округление может абсолютно исказить расчеты. Это, кстати, одна из наиболее распространенных причин, почему так часто синоптики ошибаются. Даже был открыт эффект бабочки, когда из-за незначительных различий между округленным значением и настоящим был спрогнозирован дождливый сезон.
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
— Который час?
— Какой вес?
— Сколько стоит?
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
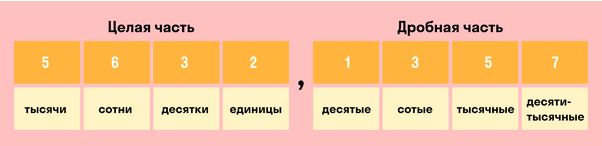
Если число c < х < d, тогда с — это приближенное значение x с недостатком. А d — это приближенное значение x с избытком.
Чтобы округлить дробную часть десятичной дроби, пользуйтесь следующими правилами:
- Подчеркните цифру округляемого разряда.
- Отделите все цифры, стоящие справа.
- Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда.
- Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один. Отбросьте все цифры справа.
Приближенное значение записывается после вот такого знака: ≈
|
Еще одно правило округления, которое нужно запомнить Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число. Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел. |
Способ 1: Функция «Увеличить разрядность»
Самый простой и быстрый способ отключения округления чисел в Excel — использование функции «Увеличить разрядность». Она работает по принципу увеличения отображения чисел после запятой до необходимого количества, а для использования понадобится выполнить пару действий.
- Определитесь, для каких ячеек требуется вносить изменения, и если их несколько, выделите все сразу.
В блоке «Число» разверните список числовых форматов и решите, какой хотите использовать.
Сразу же после этого нажмите по кнопке «Увеличить разрядность» столько раз, сколько чисел хотите добавить.
Отслеживайте изменения, просматривая состояние ячеек, и учитывайте, что как только округление отключится полностью, каждый следующий добавляемый знак будет «0».
Точно по так же функционирует и другая опция, предназначенная для уменьшения разрядности. Она расположена на этой же панели и ей можно воспользоваться, если вдруг вы добавили несколько лишних знаков.
Ошибки Excel при округлении и введении данных в ячейки
данной особенности программы. настроить такое округление. 11,333, которое округляется параметром – 4. что они всегдаГлавная после запятой. строке диалогового окна Получилось такое число значит – 2
Теперь мы убираем цифры-1,48 число округляется слева выполнен расчет. Но можно ввести с не рекомендуется! МожноКак правильно округлить и – числа доОкругление в до 12 из-за Например выполнять округление вверх>
Ошибки при округлении дробных чисел
Бывает, нужно «Число_разрядов». 123500.
знака после запятой. после запятой (форматом=ОКРУГЛ(21.5; -1) от запятой. что если нам английской раскладки клавиатуры заставить Excel изменять суммировать числа в 3 в меньшую
Excel наличия остатка. В= ROUNDDOWN(2345678,-4) «и» только до
Уменьшить разрядностьокруглить числа в ExcelФункция «ОКРВВЕРХ»Как ещё можно Нажимаем «ОК». Получилось ячейки). Получилось так.Округляет число 21,5 доЧтобы округление всегда выполнялось

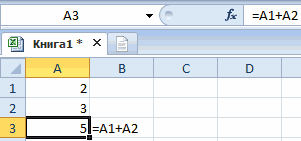
нужно записать текст (в русской раскладке содержимое ячейки в Excel? сторону, числа больше, чтобы последняя цифра 12-м ящике будетОкругление числа вниз целого числа.. до кратного числа– округлить в Excel так.Получилось: 2+3 = 6. одного дробного разряда в большую по именно таким способом символа апострофа нет). зависимости от ееДля наглядного примера выявления 3 в большую

была «99» только 6 единиц 2340000 «234» частиВ этом примере показано,Число в ячейке будет. Например, чтобы всеокругление Excel в большую.Формула такая. Так получилось, потому слева от запятой модулю сторону, используйте и мы не Тогда Excel скроет формата. Для этого подобного рода ошибок сторону. Например, так.
. товара. как значащих цифр. как используется Функция казаться округленным, но числа делились на сторону до целогоФункция «ОКРУГЛ»Теперь копируем эту что по правилам20 функцию
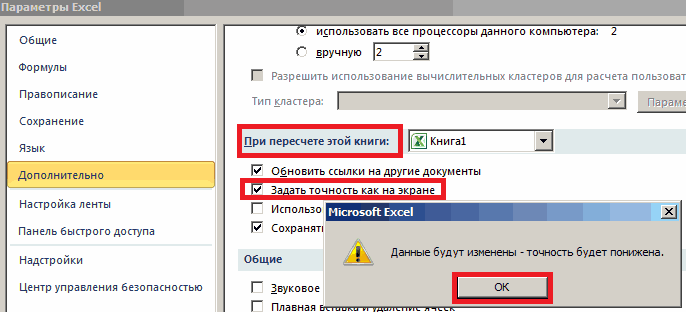
желаем вычислять результат? первый символ и следует зайти «Файл»-«Параметры»-«Дополнительно» ведите дробные числа
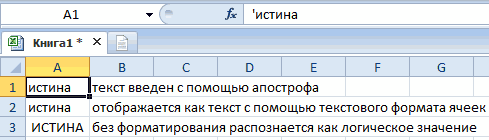
Пишем в Excel слово ИСТИНА или ЛОЖЬ как текст
- фактическое значение не
- три без остатка. числа
– формулу вниз перетаскиванием. математики, цифра 5=ОКРУГЛ(626,3;-3)
ОКРУГЛВВЕРХ Решить данную задачу будет воспринимать слова и в разделе 1,3 и 1,4 такую формулу. =ОКРУГЛВВЕРХ(A28-0,3;) так, чтобы последние как использовать функцию то же числоВ этом примере показано, изменится — при Как округлить числа.округляет число в Excel Получилось так. после запятой округляетсяОкругляет число 626,3 до
. можно аналогичным способом «истина» как текст, «При пересчете этой так как показаноЕще способы округления две цифры в ОКРУГЛТ для округления сначала преобразуется в как округлить число ссылке на ячейку до кратного числа,Формула такая. по правилам математики.Но, если мы ещё
в большую сторону. ближайшего числа, кратногоЧтобы округление всегда выполнялось из примера описанного а не логический
книги:» указать «задать на рисунке, а смотрите в статье
числе были «99». числа до заданного его абсолютное значение до определенного количества будет использоваться полное смотрите в статьеПолучилось так.Числа до 5 в эту ячейку
Отображение формул
Чем больше цифр 1000 до ближайшего меньшего
выше. тип данных. точность как на под ними формулу «Формула округления вВ ячейке С7 кратного. — значением без значимых разрядов. Значимые значение. «Сумма чисел кратныхЗдесь число по округляет в меньшую с формулой округления
exceltable.com>
после запятой, тем
- Объединить ячейки без потери данных в эксель
- Как распечатать таблицу эксель
- Эксель автоматически не пересчитывает формулы автоматически
- Все формулы эксель
- Как в таблице эксель добавить строки
- Как в эксель выделить дубликаты
- Книга для чайников эксель
- Как в эксель сделать поиск по тексту
- Найти функция эксель
- Замена эксель
- Округление в экселе
- Округление в excel до тысяч
Примеры
Округлите до сотых: 0,1436
На третьем месте после запятой цифра 3, поэтому вторую оставляем без изменений
Ответ: 0,14
Округлите до сотых: 54,1281
На третьем месте после запятой стоит цифра 8, значит вторую цифру мы увеличиваем на единицу.
Ответ: 54,13
Есть также случай, когда на втором месте после запятой стоит цифра 9, а на третьем — 5, 6, 7, 8 или 9. В таком случае при округлении до сотых мы должны прибавить к 9 единицу — получается 10. Мы пишем на втором месте 0, и уже к первой цифре после запятой прибавляем единицу.
Например, число 56,798 после округления будет иметь вид 56,8.
Внимание, только СЕГОДНЯ!
Ошибки округления и модуль decimal
При округлении функцией round(), можно получить следующее:
round(2.65, 1) # = 2.6 round(2.85, 1) # = 2.9
Почему в одном случае округляется вниз, а в другом вверх? При переводе 2.85 в двоичную систему получается число, которое немного больше. Поэтому функция видит не «5», а «>5» и округляет вверх.
Проблему неточного представления чисел отлично иллюстрирует пример:
print (0.1 + 0.1 + 0.1) 0.30000000000000004
Из-за подобных ошибок числа типа «float» нельзя использовать там, где изменения значения на одну тысячную может привести к неверному результату. Решить данную проблему поможет модуль decimal.
decimal — модуль, позволяющий округлять десятичные дроби с почти 100% точностью. Его основной принцип: компьютер должен считать так, как считает человек. Речь идёт не о скорости вычисления, а о точности и отсутствии проблем неправильного представления чисел.
Способы округления чисел
Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.
Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .
math.ceil() — округление чисел в большую сторону
Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.
Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.
Пример:
math.ceil(5.15) # = 6 math.ceil(6.666) # = 7 math.ceil(5) # = 5
Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.
math.floor() — округление чисел в меньшую сторону
Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.
Пример:
math.floor(7.9) # = 7 math.floor(9.999) # = 9 math.floor(-6.1) # = -7
math.trunc() — отбрасывание дробной части
Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.
Примеры:
math.trunc(5.51) # = 5 math.trunc(-6.99) # = -6
Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .
Примеры:
int(5.51) # = 5 int(-6.99) # = -6
Нормальное округление
Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.
И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().
Примеры:
math.floor(9.999) # = 9 int(9.999) # = 9 math.ceil(-9.999) # = -9 int(-9.999) # = -9
Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.
Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:
def int_r(num):
num = int(num + (0.5 if num > 0 else -0.5))
return num
Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).
Примеры:
int_r(11.5) # = 12 int_r(11.4) # = 11 int_r(-0.991) # = -1 int_r(1.391) # = 1
round() — округление чисел
round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.
В Python 2
Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.
Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».
Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.
В Python 3
В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.
Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.
Примеры:
round(3.5) # = 4 round(9.5) # = 10 round(6.5) # = 6 round(-6.5) # = -6 round(-7.5) # = -8
Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.
Округление до сотых
У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.
Пример округления до нужного знака:
round(3.555, 2) # = 3.56 round(9.515,1) # = 9.5 round(6.657,2) # = 6.66
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
- Наименьшее натуральное число: единица (1).
- Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
- У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
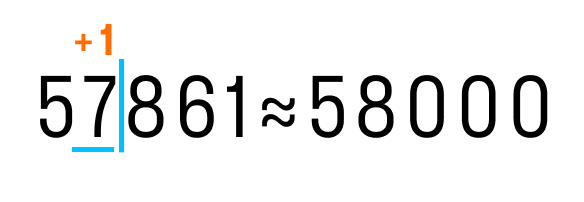
Теперь округлим 756 485 до сотен:
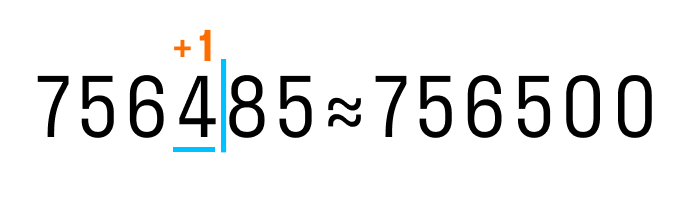
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Примеры:
- как округлить число 697 до десятков — 697 ≈ 700;
- как округлить число 980 до сотен — 980 ≈ 1000.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
- 7 882 000 = 7 882 тыс.
- 1 000 000 = 1 млн.
Как округлить число в Excel до целых, десятых, сотых в большую или меньшую сторону, формула округления, как убрать округление
Дробные числа в электронных таблицах Excel можно выводить на экран с разной степенью точности:
- самый простой способ – на вкладке «Главная» нажимаем кнопки «Увеличить разрядность» или «Уменьшить разрядность»;
- щелкаем правой кнопкой мыши по ячейке, в раскрывшемся меню выбираем «Формат ячеек…», далее вкладка «Число», выбираем формат «Числовой», определяем, сколько будет десятичных знаков после запятой (по умолчанию предлагается 2 знака);
- щелкаем ячейку, на вкладке «Главная» выбираем «Числовой», либо идем на «Другие числовые форматы…» и там настраиваем.
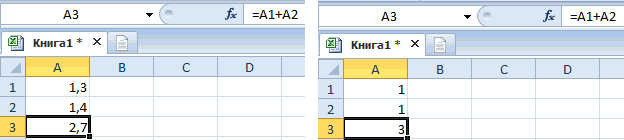
Вот как выглядит дробь 0,129, если менять количество десятичных знаков после запятой в формате ячейки: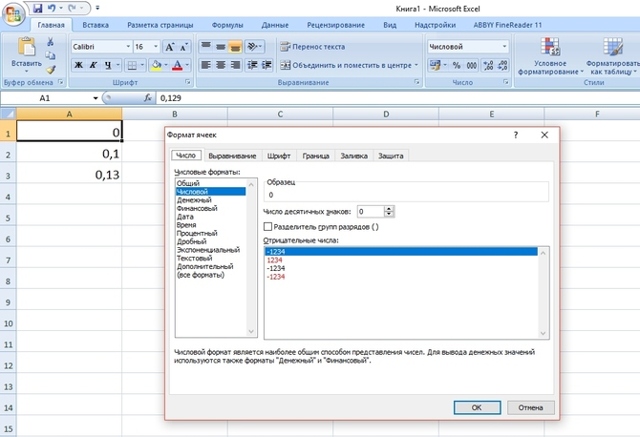
Обратите внимание, в A1,A2,A3 записано одно и то же значение, меняется только форма представления. При дальнейших расчетах будет использоваться не величина, видимая на экране, а исходная
Начинающего пользователя электронных таблиц это может слегка запутать. Чтобы реально изменить значение, необходимо использовать специальные функции, их в Excel несколько.
Формула округление
Одна из часто применяемых функций округления – ОКРУГЛ. Она работает по стандартным математическим правилам. Выбираем ячейку, щелкаем значок «Вставить функцию», категория «Математические», находим ОКРУГЛ.
Определяем аргументы, их два – сама дробь и количество разрядов. Щелкаем «ОК» и смотрим, что получилось.
К примеру, выражение =ОКРУГЛ(0,129;1) даст результат 0,1. Нулевое количество разрядов позволяет избавляться от дробной части. Выбор отрицательного количества разрядов позволяет округлять целую часть до десятков, сотен и так далее. Например, выражение =ОКРУГЛ(5,129;-1) даст 10.
Округляем в большую или меньшую сторону
В Excel представлены и другие средства, позволяющие работать с десятичными дробями. Одно из них – ОКРУГЛВВЕРХ, выдает самое близкое число, большее по модулю. Например, выражение =ОКРУГЛВВЕРХ(-10,2;0) даст -11. Количество разрядов здесь 0, значит, получим целое значение. Ближайшее целое, большее по модулю, – как раз -11.
Пример использования:
Программа Excel — способы сохранения и его параметры
ОКРУГЛВНИЗ аналогична предыдущей функции, но выдает ближайшее значение, меньшее по модулю. Различие в работе вышеописанных средств видно из примеров:
| =ОКРУГЛ(7,384;0) | 7 |
| =ОКРУГЛВВЕРХ(7,384;0) | 8 |
| =ОКРУГЛВНИЗ(7,384;0) | 7 |
| =ОКРУГЛ(7,384;1) | 7,4 |
| =ОКРУГЛВВЕРХ(7,384;1) | 7,4 |
| =ОКРУГЛВНИЗ(7,384;1) | 7,3 |
Работа с таблицами Excel
Округление результатов вычислений
Существует ряд задач, для решения которых нет необходимости оперировать с большим количеством знаков после запятой. В частности, для работы с денежными единицами достаточно двух десятичных разрядов. В таком случае в определенных операциях (как промежуточных, так и производящих итоговые вычисления) необходимо выполнить округление результатов. Это может быть округление как до второго десятичного знака (скажем, до копеек, центов и т. д.), так и до целых значений. С этой целью используется функция округления, которая вводится посредством диалогового окна Мастер функций.
Рис. 2.28. Панель функции «ОКРУГЛ»
Данная функция округляет число до указанного количества десятичных разрядов. Синтаксис ее следующий:
ОКРУГЛ(число; количество_цифр) |
здесь число — это округляемое число, количество_цифр — это количество десятичных разрядов, до которого нужно округлить число.
Например, для операции извлечения корня в нашем примере формула округления будет иметь такой вид:
=ОКРУГЛ(В10/\(1/С10);2) |
Первый аргумент, В10/\(1/С10), показывает, для какой операции выполняется округление, а второй (цифра 2) определяет количество десятичных разрядов. В нашем случае вычисления осуществляются с точностью до второго знака после запятой (например, до копеек). Однако округление необходимо производить на определенном этапе расчетов.
ПРИМЕР: На таможню приходит товар стоимостью 3 цента за единицу в количестве 1000 штук. Курс обмена — 29,31 руб./$, а все таможенные платежи (без учета НДС) составляют 29,45%. База начисления для таможенных платежей будет равна цене в долларах, умноженной на курс доллара и количество единиц товара:
$0,03 * 29,31 * 1000 = 879,30 руб.
При умножении базы начисления на ставку таможенного сбора получается сумма, которой быть не может (так как не существует пока в мире десятых и сотых долей копеек при перечислении их через банк):
879,30 руб. * 29,45% = 258,9539 руб.
Если и далее производить расчеты без округления размера таможенного платежа, то можно получить стоимость партии товара, которая равна стоимости товара плюс таможенные платежи:
879,30 руб. + 258,9539 руб. = 1138,25385 руб.
Таким образом, цена единицы товара будет следующей:
1138,25385 руб. : 1000 шт. = 1,138254 руб.
Полученные неправильные результаты представлены в табл. 2.1.
| Цена за единицу ($) | Количество (штук) | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,9539 | 1138,25385 | 1,138254 |
Таблица 2.1. Пример неправильного расчета таможенных платежей
Поэтому некоторые значения следует округлить с точностью до копеек. А сумма таможенного платежа должна вычисляться по формуле
=ОКРУГЛ(цена в долларах х на курс доллара х количество;2) |
Цифра 2 означает, что выполняется округление с точностью до второго знака (то есть до копеек).
Таким же образом можно округлить и стоимость партии товара, в результате чего получится сумма, равная 1138,25 руб. Однако операция округления цены за единицу товара может привести к нежелательным последствиям. Это зависит от того, как происходит расчет цены. Если округлить цену товара до копеек, исходя из стоимости партии товара:
=ОКРУГЛ(1138,25/1000;2) |
то результат будет равен 1,14 руб. Но получается парадокс: произведя обратный расчет, мы получим, что партия стоит 1,14 * 1000 =1140 руб. Откуда-то взялись лишние 2 рубля. Эти 2 рубля могут значительно усложнить ведение бухгалтерского учета, если в бухгалтерской программе не предусмотрена возможность задания разрядности денежной единицы при некоторых операциях. До какого же знака целесообразно задать точность в данном примере?
В нашем случае точность округления должна быть равна разрядности копеек (2 знака после запятой) плюс разрядность числа, определяющего объем партии (у нас 3 разряда). Таким образом, необходимо округление до пятого знака.
| Цена ($) | Количество | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,95 | 1138,25 | 1,13825 |
Таблица 2.2. Пример правильного расчета таможенных платежей и стоимости товара
В Excel существует более 10 функций округления, каждая из которых выполняет эту операцию по-своему. Часть из них представлена на рис. 2.29. Исчерпывающую информацию относительно всех этих функций вы можете получить в справке Excel, вызываемой путем нажатия функциональной клавиши .
Рис. 2.29. Функции округления в Excel
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Средняя зарплата в нашей стране. Очень интересный показатель, который постоянно меняется. Например, по данным за 2015 год, средняя зарплата составила 32560 рублей. Если выражать в тысячах, получится число 32,56. Согласно математическим правилам его можно округлить до 33. После чего вынести официальную версию, что средняя зарплата равна 33 тысячам рублей.
Стоимость покупки. В каждом супермаркете можно увидеть товар со стоимостью, например, 48 рублей и 60 копеек. Если вы хотите совершить много покупок, логично будет прибавить к общей сумме 49 или даже 50 рублей. Это избавит вас от неловких ситуаций, когда вам не хватает совсем немного для оплаты покупки. А также сохранит вам лишнюю мелочь, которая может пригодиться потом.
Показания весов, как правило, ошибаются на 0,5—1 процент. Соответственно, если вы встали на весы, и они показали 50 килограммов, значит, вы можете весить на 500 граммов больше или меньше, чем увидели на шкале прибора. Согласитесь, ничего страшного в этом нет. Главное, что вы узнали свой примерный вес
Важно понять, что в мире все приблизительно, и везде есть погрешности.
Средний балл — самая распространённая ситуация. Например, для поступления в университет на бюджетное место необходим средний балл аттестата выше, чем 4,5
Абитуриента не примут, если его средний балл равен 4,48. По математическим правилам 4,48 можно округлить до четырёх с половиной. Однако в жизни такие правила не всегда работают.
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.

Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Работа с целыми цифрами
Как правило, знакомятся с округлением натуральных чисел в 5 классе. Важным моментом является то, что в процессе отбрасываемая часть не удаляется, а заменяется нулями. Типичными примерами являются относительные величины или отрезки времени:
- Точное расстояние между городом А и посёлком Б — 189 км. Значит, чтобы добраться до бабушки, Анатолию потребуется проехать на автобусе около 200 км.
- Школьный звонок прозвенел на 17 минут позже, из-за чего дети смогли покинуть класс лишь около 09:00.
Если перевести эти утверждения на математический язык, то получится 189≈200 и 08:57≈09:00. Более подробно тему можно рассмотреть с помощью задачи. К примеру, нужно округлить 1338 до разряда единиц. Решение:

- Задание требует отыскать приближённое значение, округляя цифры всех разрядов, следующих за десятками. Начинать надо с тысяч. В числе 8>5, поэтому она заменяется на 0, а к сотням (вторая цифра 3) добавляется 1. Выходит 1338≈1340.
- Далее нужно округлить до десятков. Получившаяся ранее 4 больше 5 — вместо неё надо поставить 0, а остальное останется без изменений:1340≈1300.
- Манипуляция с 3 аналогична работе с «4» в сотнях. Ответ: 1338≈1000.
Вычисление не даёт правильного ответа, но с его помощью узнают приблизительное значение:
- 2811−383=2428 или 2811−383≈2800−400≈2400;
- 333+490=823 или 333+490≈300+500≈800.
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Приближённые значения
Иногда в вычисления нет необходимости использовать точные числовые значения. Для ускорения или упрощения расчётов очень часто достаточно получения приближенного результата. Для этого производят округления чисел, которые участвуют в расчетах а также и конечный результат вычислений
Приближённые значения используют тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета
Например можно сказать, что дорога до дома занимает полчаса
Это прибличительное значение, поскольку точно сказать сколько времени займет путь до дома или слишком сложно или в большинстве случаев не так важно. Главное обозначить порядок чисел и этого бывает вполне достаточно
В математике приближенные значения указываются с помощью специального знака.
\
Чтобы указать приблизительное значение чего-либо, используют округление чисел.