Ось numpy в python с подробными примерами

Нормализовать массив Numpy

Как будто теперь мы покрыли массив Numpy. Теперь мы можем генерировать массивы в соответствии с вашими предпочтениями и потребностями. В этом разделе мы сосредоточимся на нормализации этих массивов. Как уже упоминалось ранее, нормализация-это процедура приведения значений, измеренных в другой шкале, к общей шкале. Чтобы нормализовать массив 1-й, нам нужно найти нормальное значение массива. После чего нам нужно разделить массив на его нормальное значение, чтобы получить нормализованный массив.

Чтобы вычислить нормальное значение массива, мы используем именно этот синтаксис.

numpy.linalg.norm()

Теперь, когда мы закончили со всем разделом теории. Давайте посмотрим на его применение на примере.

import numpy as ppool.array(,
               )
print(a).linalg.norm(a)
print(b)/b
print(norm)

Выход:

В приведенном выше примере мы использовали тот же массив, что и сгенерированный выше. Теперь сначала мы вычислили нормальное значение массива. После вычисления нормального значения мы разделили каждый член массива на нормальное значение. Следовательно, мы получаем нормализованный массив NumPy.

Аргумент ключевого слова axis

Это устанавливает axis для сохранения образцов. Он используется только в том случае, если начальная и конечная точки относятся к типу данных массива.

По умолчанию (axis = 0) образцы будут располагаться вдоль новой оси, вставленной в начало. Мы можем использовать axis = -1, чтобы получить ось в конце.

import numpy as np

p = np.array(, ])
q = np.array(, ])

r = np.linspace(p, q, 3, axis=0)
print(r)
s = np.linspace(p, q, 3, axis=1)
print(s)

Вывод

array(,
        ],

       ,
        ],

       ,
        ]])

array(,
        ,
        ],

       ,
        ,
        ]])

В первом случае, поскольку axis = 0, мы берем пределы последовательности от первой оси.

Здесь пределы – это пары подмассивов и , а также и , берущие элементы из первой оси p и q. Теперь мы сравниваем соответствующие элементы из полученной пары, чтобы сгенерировать последовательности.

Таким образом, последовательности , ] для первой строки и ], ] для второй пары (строки), которая оценивается и объединяется для формирования , ], , ], , ]],

Во втором случае будут вставлены новые элементы в axis = 1 или столбцы. Таким образом, новая ось будет создана через последовательности столбцов. вместо последовательностей строк.

Последовательности с по и по рассматриваются и вставляются в столбцы результата, в результате чего получается , , ], , , ]].

Будучи генератором линейной последовательности, функция numpy.arange() в Python используется для генерации последовательности чисел в линейном пространстве с равномерным размером шага.

Это похоже на другую функцию, numpy.linspace() в Python, которая также генерирует линейную последовательность с одинаковым размером шага.

Давайте разберемся, как мы можем использовать эту функцию для генерации различных последовательностей.

Different methods of normalization of NumPy array

1. Normalizing using NumPy Sum

In this method, we use the NumPy ndarray sum to calculate the sum of each individual row of the array. After which we divide the elements if array by sum. Let us see this through an example.

import numpy as ppool
a=ppool.array(,
                ],dtype="float")
print(a)
b=ppool.ndarray.sum(a,axis=1)
print(b)
c=a/b
print(c)

Output:

This is another you can use for normalizing the array. This method is really effective for row-wise normalization.

2. Normalization using sklearn

Sklearn is a module of python used highly for data science and mining. Using this method also we can normalize the array. It follows a really simple procedure and let us understand it using an example.

from sklearn import preprocessing
print(preprocessing.normalize(, ]))

Output:

3. Normalization using list comprehension

You can also normalize a list in python. List comprehension, in general, offers a shorter syntax, which helps in creating the new list from the existing list. Let us look at it through an example.

list = ]
norm_list = [i / sum(j) for j in list for i in j]
print(norm_list)

Look how we were able to normalize our existing list. Here we can see that we have divided each element in the list by the sum of all elements. This also a good option for normalizing.

4. Normalization using For loop

We also carry forward the normalization process using for loop. Using for loop, we can calculate the sum of all elements. Then divide each element by that sum. Here I advise you to use the NumPy array. While carrying on the division, you may get the error as “list/int” not a suitable data-type.

import numpy as ppool
def _sum(arr):  
      
    sum=0
      
    for i in arr: 
        sum = sum + i 
          
    return(sum)  
  
arr = ppool.array( ) 
n = len(arr)  
ans = _sum(arr)  
print (ans) 
b= arr/ans
print(b)

Output:

Синтаксис

Эта функция принимает массив типа numpy (например, массив целых и логических значений NumPy).

Он возвращает новый массив numpy после фильтрации на основе условия, который представляет собой массив логических значений, подобный numpy.

Например, условие может принимать значение массива (]), который является логическим массивом типа numpy. (По умолчанию NumPy поддерживает только числовые значения, но мы также можем преобразовать их в bool).

Например, если условием является массив (]), а наш массив – a = ndarray (]), при применении условия к массиву (a ), мы получим массив ndarray (`1 2`).

import numpy as np

a = np.arange(10)
print(a) # Will only capture elements <= 2 and ignore others

Вывод:

array()

ПРИМЕЧАНИЕ. То же условие условия также может быть представлено как <= 2. Это рекомендуемый формат для массива условий, так как записывать его как логический массив очень утомительно.

Но что, если мы хотим сохранить размерность результата и не потерять элементы из нашего исходного массива? Для этого мы можем использовать numpy.where().

numpy.where(condition )

У нас есть еще два параметра x и y. Что это? По сути, это означает, что если условие выполняется для некоторого элемента в нашем массиве, новый массив будет выбирать элементы из x.

В противном случае, если это false, будут взяты элементы из y.

При этом наш окончательный выходной массив будет массивом с элементами из x, если условие = True, и элементами из y, если условие = False.

Обратите внимание, что хотя x и y необязательны, если вы указываете x, вы также ДОЛЖНЫ указать y. Это потому, что в этом случае форма выходного массива должна быть такой же, как и входной массив

ПРИМЕЧАНИЕ. Та же логика применима как для одномерных, так и для многомерных массивов. В обоих случаях мы выполняем фильтрацию по условию. Также помните, что формы x, y и условия передаются вместе.

Теперь давайте рассмотрим несколько примеров, чтобы правильно понять эту функцию.

Параметры стандартного отклонения Numpy

• a: array_like – этот параметр используется для вычисления стандартного отклонения элементов массива.
• ось: None, int или кортеж ints – Вычисление стандартного отклонения необязательно. В этом случае мы определяем ось, вдоль которой вычисляется стандартное отклонение. По умолчанию он вычисляет стандартное отклонение сплющенного массива. Если у нас есть кортеж ints, стандартное отклонение выполняется по нескольким осям, а не по одной оси или всем осям, как раньше.
• dtype: data_type – Он также необязателен при расчете стандартного отклонения. По умолчанию для массивов целочисленного типа используется тип данных float64, а массив типа float будет точно таким же, как и тип массива.
• out: ndarray – Это также необязательно при расчете стандартного отклонения. Этот параметр используется в качестве альтернативного выходного массива, в который должен быть помещен результат. Он должен иметь ту же форму, что и ожидаемый результат, но при необходимости мы можем его напечатать.
• ddof: int – Это также необязательно при расчете стандартного отклонения. Это определяет дельта-степень свободы. Делитель, который используется в вычислениях, равен N-ddof, где N представляет количество элементов. По умолчанию ddof равен нулю.
• keepdims: bool – Это необязательно. Когда значение равно true, оно оставит уменьшенную ось в виде размеров с размером один в результирующей. Когда передается значение по умолчанию, оно позволяет нестандартным значениям проходить через метод mean подклассов ndarray, но keepdims не проходят.

Синтаксис

Формат:

array = numpy.arange(start, stop, step, dtype=None)

Где:

• start -> Начальная точка (включенная) диапазона, которая по умолчанию установлена на 0;
• stop -> Конечная точка (исключенная) диапазона;
• step -> Размер шага последовательности, который по умолчанию равен 1. Это может быть любое действительное число, кроме нуля;
• dtype -> Тип выходного массива. Если dtype не указан (или указан, как None), тип данных будет выведен из типа других входных аргументов.

Давайте рассмотрим простой пример, чтобы понять это:

import numpy as np
 
a = np.arange(0.02, 2, 0.1, None)
 
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))

Это сгенерирует линейную последовательность от 0,2 (включительно) до 2 (исключено) с размером шага 0,1, поэтому в последовательности будет (2 — 0,2) / 0,1 — 1 = 20 элементов, что является длиной результирующего массив numpy.

Вывод:

Linear Sequence from 0.02 to 2: 
Length: 20

Вот еще одна строка кода, которая генерирует числа от 0 до 9 с помощью arange(), используя размер шага по умолчанию 1:

>>> np.arange(0, 10)
array()

Если размер шага равен 0, это недопустимая последовательность, поскольку шаг 0 означает, что вы делите диапазон на 0, что вызовет исключение ZeroDivisionError Exception.

import numpy as np

# Invalid Step Size!
a = np.arange(0, 10, 0)

Вывод:

ZeroDivisionError: division by zero

ПРИМЕЧАНИЕ. Эта функция немного отличается от numpy.linspace(), которая по умолчанию включает как начальную, так и конечную точки для вычисления последовательности. Он также не принимает в качестве аргумента размер шага, а принимает только количество элементов в последовательности.

Как создаются матрицы в Python?

Добавление и модификация массивов или матриц (matrix) в Python осуществляется с помощью библиотеки NumPy. Вы можете создать таким образом и одномерный, и двумерный, и многомерный массив. Библиотека обладает широким набором пакетов, которые необходимы, чтобы успешно решать различные математические задачи. Она не только поддерживает создание двумерных и многомерных массивов, но обеспечивает работу однородных многомерных матриц.

Чтобы получить доступ и начать использовать функции данного пакета, его импортируют:

import numpy as np

Функция array() — один из самых простых способов, позволяющих динамически задать одно- и двумерный массив в Python. Она создаёт объект типа ndarray:

array = np.array(/* множество элементов */)

Для проверки используется функция array.type() — принимает в качестве аргумента имя массива, который был создан.

Если хотите сделать переопределение типа массива, используйте на стадии создания dtype=np.complex:

array2 = np.array([ /*элементы*/, dtype=np.complex)

Когда стоит задача задать одномерный или двумерный массив определённой длины в Python, и его значения на данном этапе неизвестны, происходит его заполнение нулями функцией zeros(). Кроме того, можно получить матрицу из единиц через функцию ones(). При этом в качестве аргументов принимают число элементов и число вложенных массивов внутри:

np.zeros(2, 2, 2) 

К примеру, так в Python происходит задание двух массивов внутри, которые по длине имеют два элемента:

array(] 
]] 
) 

Если хотите вывести одно- либо двумерный массив на экран, вам поможет функция print(). Учтите, что если матрица слишком велика для печати, NumPy скроет центральную часть и выведет лишь крайние значения. Дабы увидеть массив полностью, используется функция set_printoptions(). При этом по умолчанию выводятся не все элементы, а происходит вывод только первой тысячи. И это значение массива указывается в качестве аргумента с ключевым словом threshold.

Обработка изображений в NumPy

Изображение является матрицей пикселей по размеру (высота х ширина).

Если изображение черно-белое, то есть представленное в полутонах, каждый пиксель может быть представлен как единственное число. Обычно между 0 (черный) и 255 (белый). Хотите обрезать квадрат размером пикселей в верхнем левом углу картинки? Просто попросите в NumPy .

Вот как выглядит фрагмент изображения:

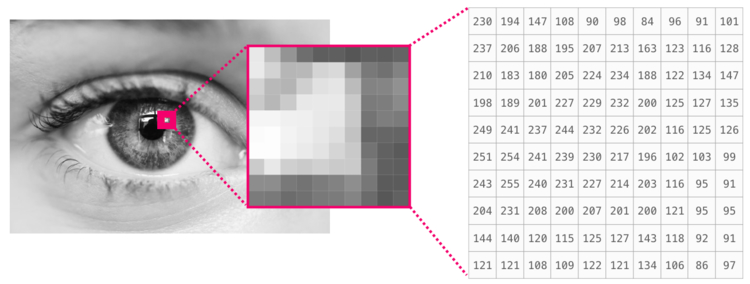
Если изображение цветное, каждый пиксель представлен тремя числами. Здесь за основу берется цветовая модель RGB — красный (R), зеленый (G) и синий (B).

В данном случае нам понадобится третья размерность, так как каждая клетка вмещает только одно число. Таким образом, цветная картинка будет представлена массивом с размерностями: (высота х ширина х 3).

Дисперсия массива без NumPy

Мы можем рассчитать дисперсию без использования модуля Numpy. Следующий пример иллюстрирует,

import math 
  
def variance(a, n): 
   
    for i in range(0 ,n): 
        sum 
    /n 
   
    for i in range(0 ,n): 
        sqDiff += ((a - mean)*(a - mean)) 
    return sqDiff / n

arr =  (arr) 
print("Variance: ", int(variance(arr, n)))

Выход –

Объяснение –

Во-первых, дисперсия зависит от квадрата разности между величиной и ее средним значением. В результате, чем больше значения удаляются от среднего, тем больше будет дисперсия. В приведенном выше примере мы создали функцию с именем variance (), которая принимает массив и его длину и возвращает его дисперсию. Сначала вычисляется среднее значение, а затем сумма

Линейная алгебра

SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.

Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.

Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.

Этот метод ожидает входную матрицу и вектор правой части:

# Import required modules/ libraries
import numpy as np
from scipy import linalg

# We are trying to solve a linear algebra system which can be given as:
#               1x + 2y =5
#               3x + 4y =6

# Create input array
A= np.array(,])

# Solution Array
B= np.array(,])

# Solve the linear algebra
X= linalg.solve(A,B)

# Print results
print(X)

# Checking Results
print("\n Checking results, following vector should be all zeros")
print(A.dot(X)-B)

1.4.1.1. What are NumPy and NumPy arrays?¶

NumPy arrays

Python objects:	high-level number objects: integers, floating point containers: lists (costless insertion and append), dictionaries (fast lookup)
NumPy provides:	extension package to Python for multi-dimensional arrays closer to hardware (efficiency) designed for scientific computation (convenience) Also known as array oriented computing

>>> import numpy as np
>>> a = np.array()
>>> a
array()

Tip

For example, An array containing:

• values of an experiment/simulation at discrete time steps
• signal recorded by a measurement device, e.g. sound wave
• pixels of an image, grey-level or colour
• 3-D data measured at different X-Y-Z positions, e.g. MRI scan
• …

Why it is useful: Memory-efficient container that provides fast numerical
operations.

In : L = range(1000)

In : %timeit i**2 for i in L
1000 loops, best of 3: 403 us per loop

In : a = np.arange(1000)

In : %timeit a**2
100000 loops, best of 3: 12.7 us per loop

NumPy Reference documentation

• On the web: https://numpy.org/doc/

• Interactive help:

  In : np.array?
  String Form:<built-in function array>
  Docstring:
  array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0, ...
  

• Looking for something:

  >>> np.lookfor('create array') 
  Search results for 'create array'
  ---------------------------------
  numpy.array
      Create an array.
  numpy.memmap
      Create a memory-map to an array stored in a *binary* file on disk.
  

  In : np.con*?
  np.concatenate
  np.conj
  np.conjugate
  np.convolve
  

Статистика¶

Команда	Описание
amin(a)	минимум в массиве или минимумы вдоль одной из осей
amax(a)	максимум в массиве или максимумы вдоль одной из осей
nanmax(a)	максимум в массиве или максимумы вдоль одной из осей (игнорируются NaN).
nanmin(a)	минимум в массиве или минимумы вдоль одной из осей (игнорируются NaN).
ptp(a)	диапазон значений (максимум — минимум) вдоль оси
average(a)	взвешенное среднее вдоль оси
mean(a)	арифметическое среднее вдоль оси
median(a)	вычисление медианы вдоль оси
std(a)	стандартное отклонение вдоль оси
corrcoef(x)	коэффициенты корреляции
correlate(a, v)	кросс-корреляция двух одномерных последовательностей
cov(m)	ковариационная матрица для данных
histogram(a)	гистограмма из набора данных
histogram2d(x, y)	двумерная гистограмма для двух наборов данных
histogramdd(sample)	многомерная гистограмма для данных
bincount(x)	число появление значения в массиве неотрицательных значений
digitize(x, bins)	возвращает индексы интервалов к которым принадлежат элементы массива

Массив нарезки

Все идет нормально; Создание и индексация массивов выглядит знакомо.

Теперь мы подошли к нарезке массивов, и это одна из функций, которая создает проблемы для начинающих массивов Python и NumPy.

Структуры, такие как списки и массивы NumPy, могут быть нарезаны. Это означает, что подпоследовательность структуры может быть проиндексирована и извлечена.

Это наиболее полезно при машинном обучении при указании входных и выходных переменных или разделении обучающих строк из строк тестирования.

Нарезка задается с помощью оператора двоеточия ‘:’ с ‘от’ а также ‘в‘Индекс до и после столбца соответственно. Срез начинается от индекса «от» и заканчивается на один элемент перед индексом «до».

Давайте рассмотрим несколько примеров.

Одномерная нарезка

Вы можете получить доступ ко всем данным в измерении массива, указав срез «:» без индексов.

При выполнении примера печатаются все элементы в массиве.

Первый элемент массива можно разрезать, указав фрагмент, который начинается с индекса 0 и заканчивается индексом 1 (один элемент перед индексом «до»)

Выполнение примера возвращает подмассив с первым элементом.

Мы также можем использовать отрицательные индексы в срезах. Например, мы можем нарезать последние два элемента в списке, начав срез с -2 (второй последний элемент) и не указав индекс «до»; это берет ломтик до конца измерения.

Выполнение примера возвращает подмассив только с двумя последними элементами.

Двумерная нарезка

Давайте рассмотрим два примера двумерного среза, которые вы, скорее всего, будете использовать в машинном обучении.

Разделение функций ввода и вывода

Распространено загруженные данные на входные переменные (X) и выходную переменную (y).

Мы можем сделать это, разрезая все строки и все столбцы до, но перед последним столбцом, затем отдельно индексируя последний столбец.

Для входных объектов мы можем выбрать все строки и все столбцы, кроме последнего, указав ‘:’ в индексе строк и: -1 в индексе столбцов.

Для выходного столбца мы можем снова выбрать все строки, используя ‘:’, и индексировать только последний столбец, указав индекс -1.

Собрав все это вместе, мы можем разделить 3-колоночный 2D-набор данных на входные и выходные данные следующим образом:

При выполнении примера печатаются разделенные элементы X и y

Обратите внимание, что X — это двумерный массив, а y — это одномерный массив

Сплит поезд и тестовые ряды

Обычно загруженный набор данных разбивают на отдельные наборы поездов и тестов.

Это разделение строк, где некоторая часть будет использоваться для обучения модели, а оставшаяся часть будет использоваться для оценки мастерства обученной модели.

Для этого потребуется разрезать все столбцы, указав «:» во втором индексе измерения. Набор обучающих данных будет содержать все строки от начала до точки разделения.

Тестовым набором данных будут все строки, начиная с точки разделения до конца измерения.

Собрав все это вместе, мы можем разделить набор данных в надуманной точке разделения 2.

При выполнении примера выбираются первые две строки для обучения и последняя строка для набора тестов.

Add array element

You can add a NumPy array element by using the append() method of the NumPy module.

The syntax of append is as follows:

numpy.append(array, value, axis)

The values will be appended at the end of the array and a new ndarray will be returned with new and old values as shown above.

The axis is an optional integer along which define how the array is going to be displayed. If the axis is not specified, the array structure will be flattened as you will see later.

Consider the following example where an array is declared first and then we used the append method to add more values to the array:

import numpy

a = numpy.array()

newArray = numpy.append (a, )

print(newArray)

The output will be like the following:

Транспонирование массивов и замена осей

Транспонирование — это особый способ изменения формы массива, который
возвращает представление исходных данных без их копирования. Массивы
имеют метод , а также специальный атрибут :

In : arr = np.arange(15).reshape((3, 5))

In : arr
Out: 
array(,
       ,
       ])

In : arr.T
Out: 
array(,
       ,
       ,
       ,
       ])

При выполнении матричных вычислений эта процедура может выполняться
очень часто, например, при вычислении произведения матриц с помощью
функции :

In : arr = np.random.randn(6, 3)

In : arr
Out: 
array(,
       ,
       ,
       ,
       ,
       ])

In : np.dot(arr.T, arr)
Out: 
array(,
       ,
       ])

Для массивов большей размерности метод принимает кортеж с
номерами осей, задающий перестановку осей:

In : arr = np.arange(16).reshape((2, 2, 4))

In : arr
Out: 
array(,
        ],

       ,
        ]])

In : arr.transpose((1, , 2))
Out: 
array(,
        ],

       ,
        ]])

Здесь оси были переупорядочены следующим образом: вторая ось стала
первой, первая ось — второй, а последняя осталась без изменений.

Простое транспонирование с помощью является частным случаем
замены осей. Массивы имеют метод , который получает пару
номеров осей и переставляет указанные оси.

In : arr.swapaxes(1, 2)
Out: 
array(,
        ,
        ,
        ],

       ,
        ,
        ,
        ]])

Метод возвращает представление данных без копирования.

• ← Prev
• Next →

1.4.1.5. Indexing and slicing¶

The items of an array can be accessed and assigned to the same way as
other Python sequences (e.g. lists):

>>> a = np.arange(10)
>>> a
array()
>>> a], a2], a-1
(0, 2, 9)

Warning

Indices begin at 0, like other Python sequences (and C/C++).
In contrast, in Fortran or Matlab, indices begin at 1.

The usual python idiom for reversing a sequence is supported:

>>> a)

For multidimensional arrays, indices are tuples of integers:

>>> a = np.diag(np.arange(3))
>>> a
array(,
       ,
       ])
>>> a1, 1
1
>>> a2, 1 = 10 # third line, second column
>>> a
array(,
       ,
       ])
>>> a1
array()

Note

• In 2D, the first dimension corresponds to rows, the second
  to columns.
• for multidimensional , is interpreted by
  taking all elements in the unspecified dimensions.

Slicing: Arrays, like other Python sequences can also be sliced:

>>> a = np.arange(10)
>>> a
array()
>>> a293 # 
array()

Note that the last index is not included! :

>>> a)

All three slice components are not required: by default, start is 0,
end is the last and step is 1:

>>> a13
array()
>>> a)
>>> a3:]
array()

A small illustrated summary of NumPy indexing and slicing…

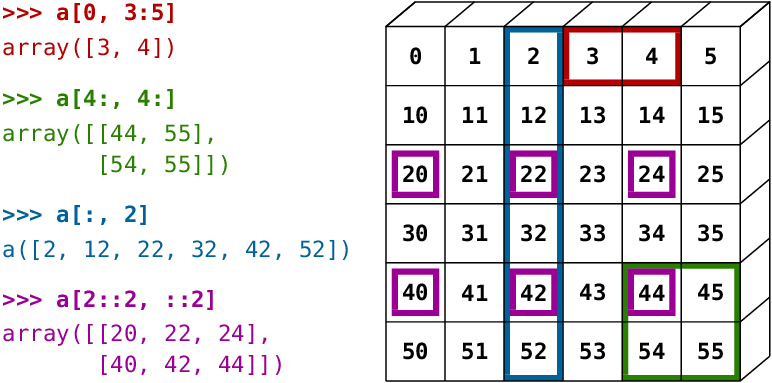
You can also combine assignment and slicing:

>>> a = np.arange(10)
>>> a5:] = 10
>>> a
array()
>>> b = np.arange(5)
>>> a5:] = b)

Exercise: Indexing and slicing

• Try the different flavours of slicing, using , and
  : starting from a linspace, try to obtain odd numbers
  counting backwards, and even numbers counting forwards.

• Reproduce the slices in the diagram above. You may
  use the following expression to create the array:

  >>> np.arange(6) + np.arange(, 51, 10),
         ,
         ,
         ,
         ,
         ])
  

Exercise: Array creation

Create the following arrays (with correct data types):

,
 1, 1, 1, 1],
 1, 1, 1, 2],
 1, 6, 1, 1]]

,
 2., , , , ],
 , 3., , , ],
 , , 4., , ],
 , , , 5., ],
 , , , , 6.]]

Par on course: 3 statements for each

Hint: Individual array elements can be accessed similarly to a list,
e.g. or .

Hint: Examine the docstring for .

Пример

Давайте теперь объединим все это в простой пример, чтобы продемонстрировать линейность последовательностей, генерируемых numpy.arange().

Следующий код отображает 2 линейные последовательности между и с помощью numpy.arange(), чтобы показать, что последовательность генерирует единообразие, поэтому результирующие массивы являются линейными.

import numpy as np
import matplotlib.pyplot as plt

y = np.zeros(5)

# Construct two linear sequences
# First one has a step size of 4 units
x1 = np.arange(0, 20, 4)

# Second one has a step size of 2 units
x2 = np.arange(0, 10, 2)

# Plot (x1, )
plt.plot(x1, y, 'o')

# Plot (x2, )
plt.plot(x2, y + 0.5, 'o')

# Set limit for y on the plot
plt.ylim()

plt.show()

Вывод

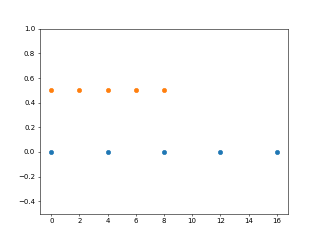
Как вы можете видеть, оранжевые точки представляют линейную последовательность от 0 до 10 с размером шага 2 единицы, но поскольку 10 не включено, последовательность равна . Точно так же синие точки представляют последовательность .